
AllQuestion and Answers: Page 1213
Question Number 95707 Answers: 1 Comments: 3

Question Number 95703 Answers: 1 Comments: 1
Question Number 95699 Answers: 1 Comments: 4
Question Number 95697 Answers: 2 Comments: 0
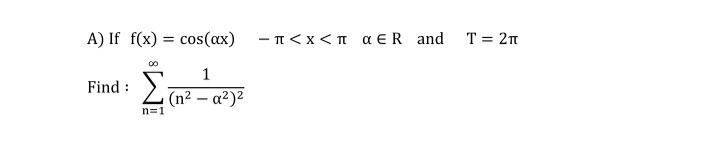
Question Number 95695 Answers: 1 Comments: 0
Question Number 95694 Answers: 1 Comments: 0
Question Number 95693 Answers: 1 Comments: 0
Question Number 95692 Answers: 1 Comments: 0
Question Number 95691 Answers: 0 Comments: 1
Question Number 95690 Answers: 0 Comments: 0
Question Number 95679 Answers: 0 Comments: 2
Question Number 95677 Answers: 1 Comments: 0
Question Number 95676 Answers: 0 Comments: 0
Question Number 95673 Answers: 0 Comments: 2
Question Number 95670 Answers: 0 Comments: 0

Question Number 95668 Answers: 1 Comments: 2
Question Number 95662 Answers: 1 Comments: 5
Question Number 95653 Answers: 2 Comments: 0
Question Number 95650 Answers: 1 Comments: 0
Question Number 95648 Answers: 0 Comments: 8
Question Number 95644 Answers: 0 Comments: 0
Question Number 95643 Answers: 1 Comments: 0
Question Number 95639 Answers: 1 Comments: 1
Question Number 95638 Answers: 1 Comments: 0
Question Number 95636 Answers: 2 Comments: 0
Question Number 95635 Answers: 1 Comments: 0
Pg 1208 Pg 1209 Pg 1210 Pg 1211 Pg 1212 Pg 1213 Pg 1214 Pg 1215 Pg 1216 Pg 1217
