
AllQuestion and Answers: Page 1212
Question Number 95801 Answers: 2 Comments: 0
Question Number 95800 Answers: 1 Comments: 2
Question Number 95789 Answers: 1 Comments: 1
Question Number 95786 Answers: 1 Comments: 2
Question Number 95785 Answers: 0 Comments: 0
Question Number 95784 Answers: 0 Comments: 0
Question Number 95782 Answers: 0 Comments: 2
Question Number 95780 Answers: 0 Comments: 0

Question Number 95779 Answers: 2 Comments: 0
Question Number 95773 Answers: 4 Comments: 0
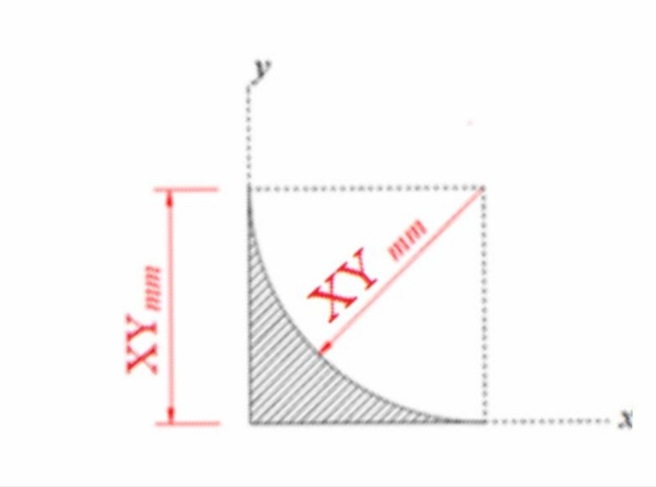
Question Number 95772 Answers: 0 Comments: 3
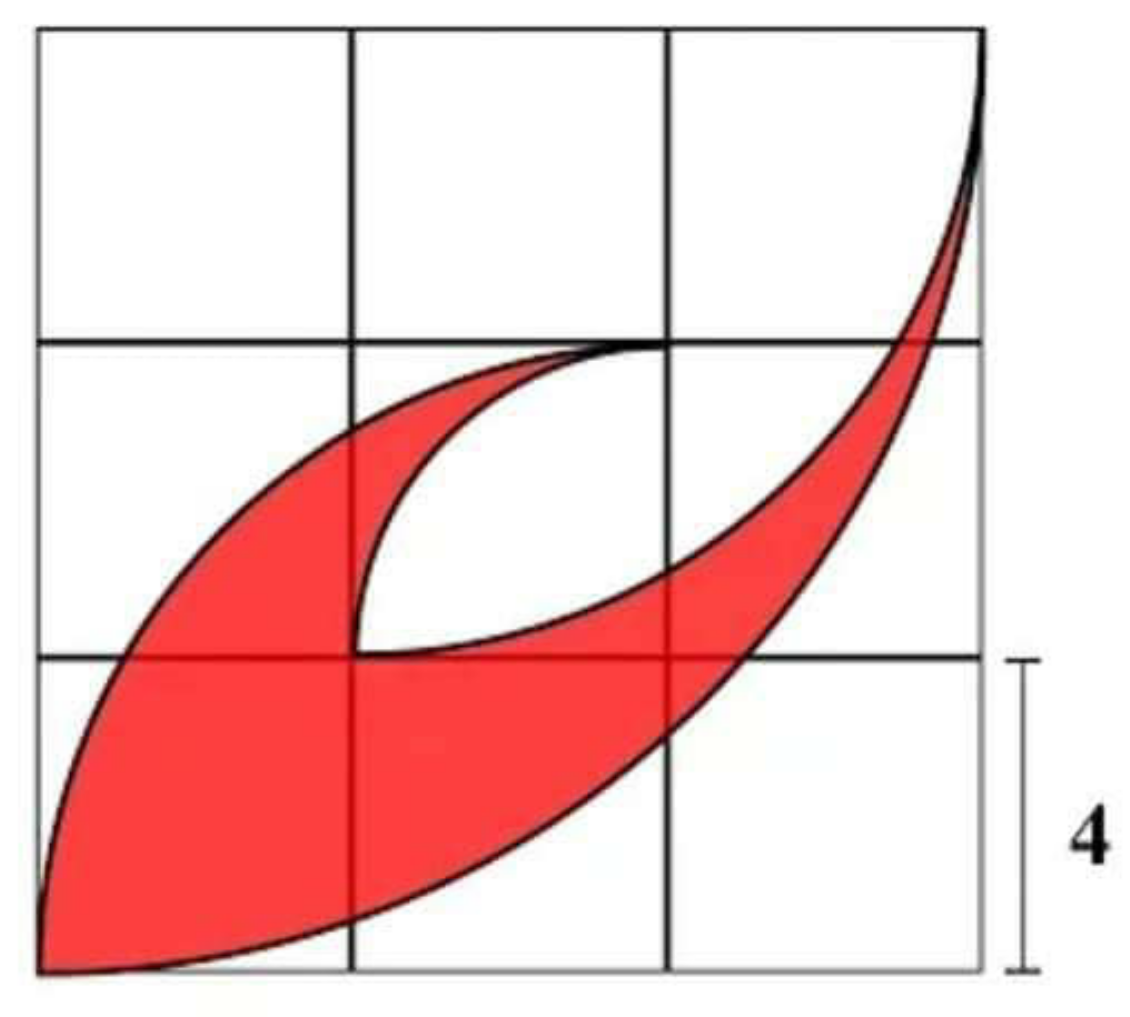
Question Number 95770 Answers: 0 Comments: 8
Question Number 95768 Answers: 0 Comments: 1
Question Number 95767 Answers: 1 Comments: 0

Question Number 95766 Answers: 0 Comments: 1
Question Number 95765 Answers: 0 Comments: 3
Question Number 95763 Answers: 0 Comments: 3
$$\int\:{x}\:\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx}\:? \\ $$
Question Number 95760 Answers: 1 Comments: 0
Question Number 95748 Answers: 2 Comments: 0
$$\mathrm{y}''\:=\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x} \\ $$
Question Number 95742 Answers: 2 Comments: 2
Question Number 95738 Answers: 1 Comments: 2
Question Number 95846 Answers: 1 Comments: 0
Question Number 95726 Answers: 0 Comments: 1
Question Number 95723 Answers: 3 Comments: 1

Question Number 95722 Answers: 2 Comments: 0
Question Number 95707 Answers: 1 Comments: 3

Pg 1207 Pg 1208 Pg 1209 Pg 1210 Pg 1211 Pg 1212 Pg 1213 Pg 1214 Pg 1215 Pg 1216
