
AllQuestion and Answers: Page 1211
Question Number 95531 Answers: 0 Comments: 4
$$\frac{\mathrm{tanx}×\mathrm{ctg2x}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}=? \\ $$
Question Number 95524 Answers: 0 Comments: 4
$$\frac{\mathrm{1}}{\mathrm{sin10}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{cos10}}=? \\ $$
Question Number 95520 Answers: 0 Comments: 0
Question Number 95518 Answers: 0 Comments: 0

Question Number 95515 Answers: 1 Comments: 0
Question Number 95512 Answers: 0 Comments: 3
Question Number 95509 Answers: 2 Comments: 0
Question Number 95502 Answers: 1 Comments: 3
Question Number 95495 Answers: 2 Comments: 0
Question Number 95494 Answers: 0 Comments: 0

Question Number 95485 Answers: 0 Comments: 2

Question Number 95592 Answers: 0 Comments: 1
Question Number 95473 Answers: 1 Comments: 0

Question Number 95471 Answers: 0 Comments: 1
Question Number 95469 Answers: 0 Comments: 1
Question Number 95465 Answers: 1 Comments: 0
Question Number 95464 Answers: 0 Comments: 8

Question Number 95456 Answers: 0 Comments: 0
Question Number 95449 Answers: 1 Comments: 7
Question Number 95447 Answers: 1 Comments: 0
Question Number 95440 Answers: 1 Comments: 0
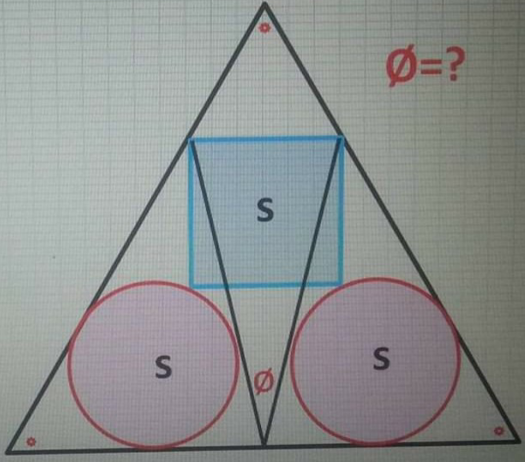
Question Number 95436 Answers: 1 Comments: 0
Question Number 95424 Answers: 2 Comments: 1
Question Number 95420 Answers: 0 Comments: 7
Question Number 95417 Answers: 1 Comments: 0
Question Number 95416 Answers: 1 Comments: 4
Pg 1206 Pg 1207 Pg 1208 Pg 1209 Pg 1210 Pg 1211 Pg 1212 Pg 1213 Pg 1214 Pg 1215
