Question and Answers Forum

AllQuestion and Answers: Page 1210

Question Number 95180 Answers: 0 Comments: 1

Question Number 95167 Answers: 0 Comments: 2

the first term in a geometric series is (((2x + 7))/(2x−5)) and the common ratio is (((2x−5))/(2x + 7)) find the set of values of x for which all the terms are possible.

$$\mathrm{the}\:\mathrm{first}\:\mathrm{term}\:\mathrm{in}\:\mathrm{a}\:\mathrm{geometric}\:\mathrm{series}\:\mathrm{is}\:\frac{\left(\mathrm{2}{x}\:+\:\mathrm{7}\right)}{\mathrm{2}{x}−\mathrm{5}}\:\mathrm{and}\:\mathrm{the}\:\mathrm{common}\:\mathrm{ratio}\:\mathrm{is} \\ $$$$\:\frac{\left(\mathrm{2}{x}−\mathrm{5}\right)}{\mathrm{2}{x}\:+\:\mathrm{7}}\:\mathrm{find}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:{x}\:\mathrm{for}\:\mathrm{which}\:\mathrm{all}\:\mathrm{the}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{possible}. \\ $$

Question Number 95164 Answers: 0 Comments: 3

if a_k =tan (θ+((kπ)/n)), find ((Σ_(k=1) ^n a_k )/(Π_(k=1) ^n a_k ))=?

$${if}\:{a}_{{k}} =\mathrm{tan}\:\left(\theta+\frac{{k}\pi}{{n}}\right), \\ $$$${find}\:\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} }{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{a}_{{k}} }=? \\ $$

Question Number 95159 Answers: 1 Comments: 1

((8−x))^(1/(3 )) + (√x) = 2

$$\sqrt[{\mathrm{3}\:\:}]{\mathrm{8}−\mathrm{x}}\:+\:\sqrt{\mathrm{x}}\:=\:\mathrm{2}\: \\ $$

Question Number 95158 Answers: 0 Comments: 0

find the domain and range f(x)=⌊(1/(sin{x}))⌋

$${find}\:{the}\:{domain}\:{and}\:{range} \\ $$$${f}\left({x}\right)=\lfloor\frac{\mathrm{1}}{{sin}\left\{{x}\right\}}\rfloor \\ $$

Question Number 95150 Answers: 1 Comments: 0

how do you solve f(x) +2 f((1/(1−x))) = x for f ?

$$\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{f}\left(\mathrm{x}\right)\:+\mathrm{2}\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\mathrm{x}\: \\ $$$$\mathrm{for}\:\mathrm{f}\:?\: \\ $$

Question Number 95145 Answers: 1 Comments: 0

what is the sum of (1/(14)) + (1/(35)) +(1/(65)) + (1/(104)) + ... ?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{14}}\:+\:\frac{\mathrm{1}}{\mathrm{35}}\:+\frac{\mathrm{1}}{\mathrm{65}}\:+\:\frac{\mathrm{1}}{\mathrm{104}}\:+\:...\:? \\ $$

Question Number 95140 Answers: 0 Comments: 2

what is range of a function f(x)= ((x+1)/(√(x^2 −1)))

$$\mathrm{what}\:\mathrm{is}\:\mathrm{range}\:\mathrm{of}\:\mathrm{a}\:\mathrm{function}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{x}+\mathrm{1}}{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\: \\ $$

Question Number 95133 Answers: 1 Comments: 0

lim_(x→∞) (x^2 .e^( −2x) ) = ?

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{x}^{\mathrm{2}} .\mathrm{e}^{\:−\mathrm{2x}} \right)\:=\:? \\ $$

Question Number 95132 Answers: 0 Comments: 0

dolve xy^(′′) +(1−x^2 )y^′ +3y =x e^(−2x)

$$\mathrm{dolve}\:\:\mathrm{xy}^{''} \:+\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{y}^{'} \:+\mathrm{3y}\:=\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} \\ $$

Question Number 95127 Answers: 0 Comments: 1

Question Number 95121 Answers: 1 Comments: 1

Question Number 95119 Answers: 1 Comments: 0

Solve the differential equations:− ★.(x sin x+cos x)(d^2 y/dx^2 ) −x cos x(dy/dx) + y cos x=0.

$$\:\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equations}:− \\ $$$$\bigstar.\left(\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:−\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\:\mathrm{y}\:\mathrm{cos}\:\mathrm{x}=\mathrm{0}. \\ $$

Question Number 95115 Answers: 2 Comments: 0

∫ e^( x) (√(1+e^( 2x) )) dx = ?

$$\int\:\mathrm{e}^{\:{x}} \:\sqrt{\mathrm{1}+{e}^{\:\mathrm{2}{x}} }\:{dx}\:=\:?\: \\ $$

Question Number 95108 Answers: 1 Comments: 0

∣1−log _(((1/6))) (x)∣ +2 = ∣3 −log _(((1/6))) (3)∣

$$\mid\mathrm{1}−\mathrm{log}\:_{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)} \left(\mathrm{x}\right)\mid\:+\mathrm{2}\:=\:\mid\mathrm{3}\:−\mathrm{log}\:_{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)} \left(\mathrm{3}\right)\mid\: \\ $$

Question Number 95106 Answers: 2 Comments: 0

{ ((x+y+z = 7)),((x^2 +y^2 +z^2 = 49)),((x^3 +y^3 +z^3 = 7)) :} find x; y ; z

$$\begin{cases}{{x}+{y}+{z}\:=\:\mathrm{7}}\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:=\:\mathrm{49}}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \:=\:\mathrm{7}}\end{cases} \\ $$$${find}\:{x};\:\mathrm{y}\:;\:{z}\: \\ $$

Question Number 95098 Answers: 2 Comments: 0

[ (y/(x^2 +y^2 )) + (x/(x^2 +y^2 )) ] dx + [(y/(x^2 +y^2 ))−(x/(x^2 +y^2 )) ]dy=0

$$\left[\:\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:+\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\right]\:\mathrm{dx}\:+\:\left[\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\right]\mathrm{dy}=\mathrm{0} \\ $$

Question Number 95093 Answers: 2 Comments: 0

Solve: x^2 + y^2 = 13 ....... (i) 2x^2 + 3y = 2xy^2 ....... (ii)

$$\mathrm{Solve}: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:+\:\:\mathrm{y}^{\mathrm{2}} \:\:=\:\:\mathrm{13}\:\:\:\:\:\:\:\:\:\:.......\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\mathrm{2x}^{\mathrm{2}} \:\:+\:\:\mathrm{3y}\:\:=\:\:\mathrm{2xy}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:.......\:\left(\mathrm{ii}\right) \\ $$

Question Number 95068 Answers: 1 Comments: 3

Solve the differential equations−: 1. (dy/dx) = sin(x+y)+ cos(x+y)

$$\:\:\:\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equations}−: \\ $$$$\:\:\:\mathrm{1}.\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{sin}\left(\mathrm{x}+\mathrm{y}\right)+\:\mathrm{cos}\left(\mathrm{x}+\mathrm{y}\right) \\ $$$$\: \\ $$

Question Number 95062 Answers: 0 Comments: 7

solve for x, y, z ∈C such that ∣x∣=∣y∣=∣z∣=1 x+y+z=1 xyz=1

$${solve}\:{for}\:{x},\:{y},\:{z}\:\in\mathbb{C}\:{such}\:{that} \\ $$$$\mid{x}\mid=\mid{y}\mid=\mid{z}\mid=\mathrm{1} \\ $$$${x}+{y}+{z}=\mathrm{1} \\ $$$${xyz}=\mathrm{1} \\ $$

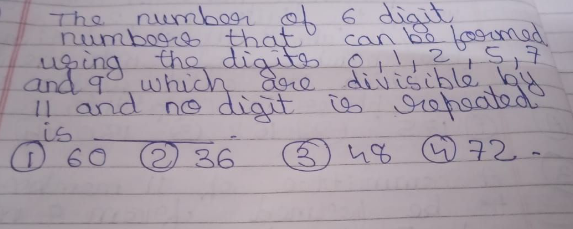
Question Number 95060 Answers: 3 Comments: 0

Evaluate ∫_0 ^∞ arcsin(e^(-x) ) dx ∫_0 ^∞ arccos(1-2e^(-x) ) dx and Step Up Evaluate ∫_0 ^∞ arccos(1-e^(-x) ) dx ∫_(-t) ^t arctan(e^(-x) ) dx

$${Evaluate} \\ $$$$\int_{\mathrm{0}} ^{\infty} {arcsin}\left({e}^{-{x}} \right)\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} {arccos}\left(\mathrm{1}-\mathrm{2}{e}^{-{x}} \right)\:{dx} \\ $$$${and}\:{Step}\:{Up} \\ $$$${Evaluate} \\ $$$$\int_{\mathrm{0}} ^{\infty} {arccos}\left(\mathrm{1}-{e}^{-{x}} \right)\:{dx} \\ $$$$\int_{-{t}} ^{{t}} {arctan}\left({e}^{-{x}} \right)\:{dx} \\ $$

Question Number 95053 Answers: 0 Comments: 2

Question Number 95048 Answers: 0 Comments: 1

a_1 =−(1/(30)) a_2 =−(1/(12)) a_3 =−(1/6) a_4 =−(7/(24)) a_5 =−(7/(15)) a_6 =−(7/(10)) a_7 =−1 find a_k

$${a}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{30}} \\ $$$${a}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${a}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${a}_{\mathrm{4}} =−\frac{\mathrm{7}}{\mathrm{24}} \\ $$$${a}_{\mathrm{5}} =−\frac{\mathrm{7}}{\mathrm{15}} \\ $$$${a}_{\mathrm{6}} =−\frac{\mathrm{7}}{\mathrm{10}} \\ $$$${a}_{\mathrm{7}} =−\mathrm{1} \\ $$$${find}\:{a}_{{k}} \\ $$

Question Number 95020 Answers: 1 Comments: 1

Question Number 95014 Answers: 0 Comments: 10

If y_(n + 1) − y_n = 6, and y_0 = 7 Find y_n

$$\boldsymbol{\mathrm{If}}\:\:\:\:\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{n}}\:\:+\:\:\mathrm{1}} \:\:−\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{n}}} \:\:\:=\:\:\:\mathrm{6},\:\:\:\:\:\:\:\boldsymbol{\mathrm{and}}\:\:\:\:\:\boldsymbol{\mathrm{y}}_{\mathrm{0}} \:\:=\:\:\:\mathrm{7} \\ $$$$\boldsymbol{\mathrm{Find}}\:\:\:\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{n}}} \\ $$

Question Number 95012 Answers: 0 Comments: 1

∫(1/(√((x−1)(x−2)(x−3)(x−4))))dx

$$\int\frac{\mathrm{1}}{\sqrt{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}}{dx} \\ $$

Pg 1205 Pg 1206 Pg 1207 Pg 1208 Pg 1209 Pg 1210 Pg 1211 Pg 1212 Pg 1213 Pg 1214

Contact: info@tinkutara.com