
AllQuestion and Answers: Page 1205
Question Number 96192 Answers: 0 Comments: 2
Question Number 96189 Answers: 3 Comments: 0
Question Number 96185 Answers: 1 Comments: 0
Question Number 96182 Answers: 1 Comments: 0
$${x}^{\mathrm{2}} {y}''−{xy}'+\mathrm{y}\:=\:\mathrm{0}\: \\ $$
Question Number 96175 Answers: 1 Comments: 1
$$\int\frac{{dx}}{\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}}=? \\ $$
Question Number 96171 Answers: 0 Comments: 2
Question Number 96161 Answers: 1 Comments: 1
Question Number 96155 Answers: 1 Comments: 4

Question Number 96148 Answers: 2 Comments: 14

Question Number 96140 Answers: 1 Comments: 5
Question Number 96138 Answers: 0 Comments: 1
$${xy}'\:+\:{y}^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} {e}^{{x}} \: \\ $$
Question Number 96135 Answers: 0 Comments: 5
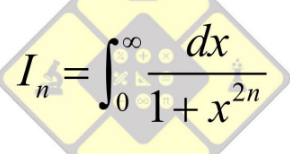
Question Number 96128 Answers: 1 Comments: 0
Question Number 96131 Answers: 1 Comments: 0
Question Number 96125 Answers: 1 Comments: 0
$$\mathrm{4x}^{\mathrm{2}} \mathrm{y}''\:+\mathrm{12xy}'\:+\:\mathrm{3y}\:=\:\mathrm{0} \\ $$
Question Number 96117 Answers: 2 Comments: 0
Question Number 96108 Answers: 0 Comments: 0
$${are}\:{the}\:{system}\:\left({z},+,\leqslant\right){is}\:{orderd}\:{integral}\:{domain}\:? \\ $$
Question Number 96106 Answers: 0 Comments: 1

Question Number 96097 Answers: 1 Comments: 0

Question Number 96092 Answers: 0 Comments: 4
$${find}\:\int\frac{{dx}}{{tan}^{−\mathrm{1}} \left({x}\right)} \\ $$
Question Number 97266 Answers: 2 Comments: 1
Question Number 96089 Answers: 2 Comments: 0

Question Number 96083 Answers: 1 Comments: 0
Question Number 96078 Answers: 0 Comments: 0
Question Number 96076 Answers: 2 Comments: 0
$$\int\:\mathrm{3x}.\mathrm{2}^{\mathrm{x}} \:\mathrm{dx}\:?\: \\ $$
Question Number 96072 Answers: 1 Comments: 0
Pg 1200 Pg 1201 Pg 1202 Pg 1203 Pg 1204 Pg 1205 Pg 1206 Pg 1207 Pg 1208 Pg 1209
