
AllQuestion and Answers: Page 1204
Question Number 96730 Answers: 1 Comments: 0
Question Number 96729 Answers: 2 Comments: 1
Question Number 96746 Answers: 3 Comments: 2
Question Number 96715 Answers: 1 Comments: 0
Question Number 96713 Answers: 1 Comments: 0
$${y}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{dy}}{{dx}} \\ $$
Question Number 96712 Answers: 1 Comments: 0

Question Number 96705 Answers: 1 Comments: 0
Question Number 96699 Answers: 0 Comments: 2
$$\int\:\frac{\mathrm{tan}^{\mathrm{3}} \left(\mathrm{ln}\:{x}\right)}{{x}}\:{dx}\:=\:?? \\ $$
Question Number 96693 Answers: 1 Comments: 0
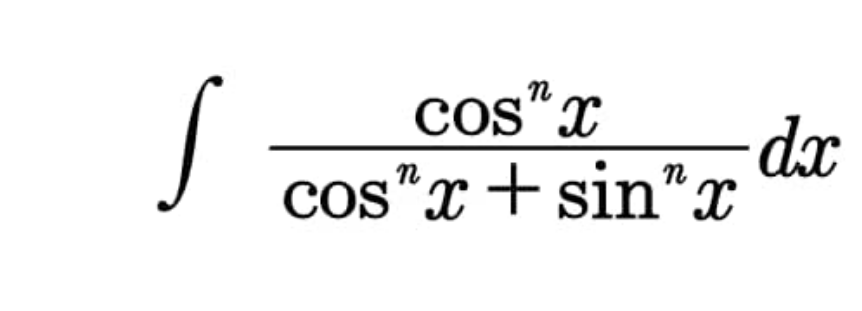
Question Number 96685 Answers: 1 Comments: 0
Question Number 96684 Answers: 2 Comments: 0
Question Number 96682 Answers: 1 Comments: 4

Question Number 96679 Answers: 1 Comments: 0
Question Number 96672 Answers: 0 Comments: 1
$${Evaluate}\:: \\ $$$$\int\:\frac{{log}_{{x}} {a}}{{x}}\:{dx} \\ $$
Question Number 96671 Answers: 1 Comments: 0

Question Number 96669 Answers: 2 Comments: 0
Question Number 96667 Answers: 2 Comments: 0
Question Number 96660 Answers: 1 Comments: 0
Question Number 96659 Answers: 1 Comments: 0
Question Number 96658 Answers: 1 Comments: 0
Question Number 96657 Answers: 2 Comments: 0
Question Number 96656 Answers: 1 Comments: 0
Question Number 96655 Answers: 1 Comments: 0
Question Number 96652 Answers: 1 Comments: 0
Question Number 96650 Answers: 1 Comments: 0
Question Number 96637 Answers: 0 Comments: 1
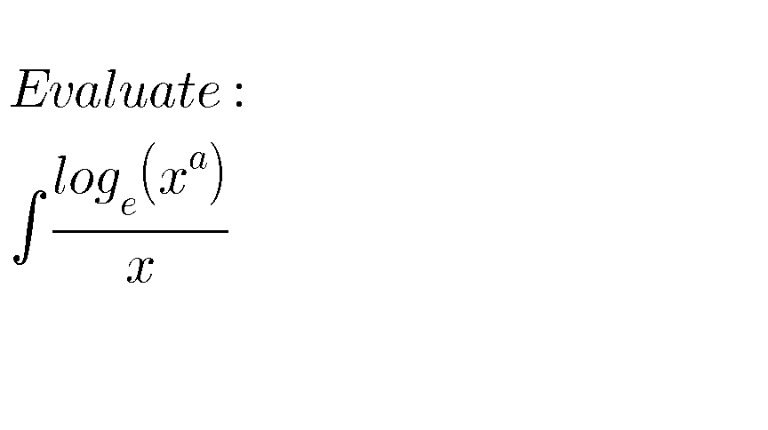
Pg 1199 Pg 1200 Pg 1201 Pg 1202 Pg 1203 Pg 1204 Pg 1205 Pg 1206 Pg 1207 Pg 1208
