
AllQuestion and Answers: Page 1202
Question Number 96554 Answers: 1 Comments: 2
Question Number 96548 Answers: 0 Comments: 1

Question Number 96543 Answers: 1 Comments: 0

Question Number 96542 Answers: 0 Comments: 6

Question Number 96538 Answers: 1 Comments: 0

Question Number 96530 Answers: 0 Comments: 1
Question Number 96527 Answers: 2 Comments: 1
Question Number 96524 Answers: 0 Comments: 1
Question Number 96523 Answers: 0 Comments: 0
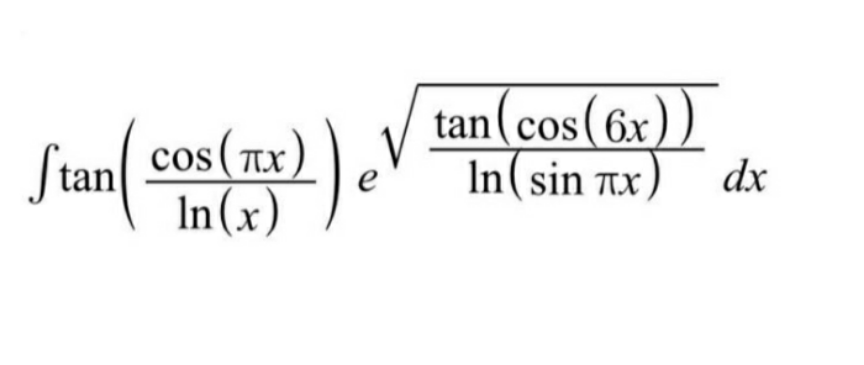
Question Number 96514 Answers: 1 Comments: 3
Question Number 96508 Answers: 1 Comments: 0

Question Number 96505 Answers: 2 Comments: 2
Question Number 96500 Answers: 2 Comments: 0
Question Number 96495 Answers: 2 Comments: 0
Question Number 96489 Answers: 1 Comments: 0
Question Number 96481 Answers: 0 Comments: 5
Question Number 96479 Answers: 1 Comments: 0
Question Number 96467 Answers: 1 Comments: 0
Question Number 96466 Answers: 0 Comments: 0

Question Number 96460 Answers: 1 Comments: 8

Question Number 96454 Answers: 1 Comments: 0

Question Number 96441 Answers: 1 Comments: 1

Question Number 96437 Answers: 1 Comments: 0

Question Number 96436 Answers: 0 Comments: 0
Question Number 96429 Answers: 1 Comments: 0

Question Number 96428 Answers: 2 Comments: 0
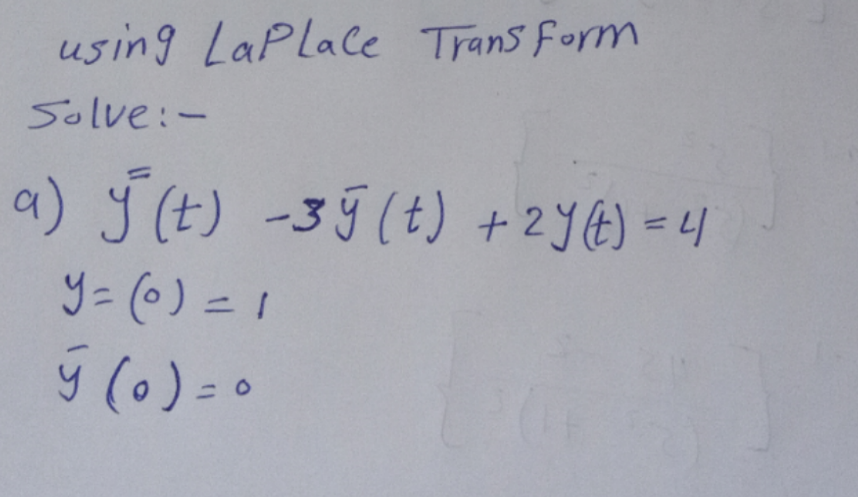
Pg 1197 Pg 1198 Pg 1199 Pg 1200 Pg 1201 Pg 1202 Pg 1203 Pg 1204 Pg 1205 Pg 1206
