Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1201

Question Number 88339 Answers: 3 Comments: 3

∫( (√(tan x )) + (√(cot x)) )dx = ?

$\int (\sqrt{\tan x} + \sqrt{\cot x}) d x = ?$

Question Number 88329 Answers: 0 Comments: 4

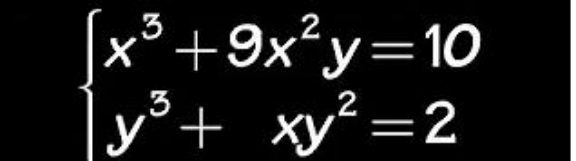
Question Number 88332 Answers: 0 Comments: 0

Question Number 88314 Answers: 2 Comments: 1

( a,b )are complex numbers and a^2 +ab+b^2 =0 find ((a/(a+b)))^(2020) +((b/(a+b)))^(2020)

$(a, b) a r e c o m p l e x n u m b e r s a n d a^{2} + a b + b^{2} = 0$ $f i n d {(\frac{a}{a + b})}^{2020} + {(\frac{b}{a + b})}^{2020}$

Question Number 88310 Answers: 1 Comments: 1

Question Number 88306 Answers: 0 Comments: 5

Question Number 88301 Answers: 0 Comments: 2

A circle touches the four sides of quadrilateral ABCD. Show/prove that AB+CD=BC+DA. Please help.

$A c i r c l e t o u c h e s t h e f o u r s i d e s$ $o f q u a d r i l a t e r a l A B C D . Show / prove$ $that A B + C D = B C + D A .$ $Please help .$

Question Number 88300 Answers: 0 Comments: 0

A circle touches the four sides of quadrilateral ABCD. Show/prove that AB+CD=BC+DA. Please help.

$A c i r c l e t o u c h e s t h e f o u r s i d e s$ $o f q u a d r i l a t e r a l A B C D . Show / prove$ $that A B + C D = B C + D A .$ $Please help .$

Question Number 88307 Answers: 1 Comments: 0

∫(x^2 /(x^2 −(5/2)x−(3/2))) dx

$\int \frac{x^{2}}{x^{2} - \frac{5}{2} x - \frac{3}{2}} d x$

Question Number 88289 Answers: 0 Comments: 5

Question Number 88288 Answers: 1 Comments: 1

Question Number 88286 Answers: 0 Comments: 1

Question Number 88272 Answers: 1 Comments: 1

Question Number 88270 Answers: 0 Comments: 1

Question Number 88263 Answers: 1 Comments: 1

prove that ∣((e^z −e^(−z) )/2)∣^2 +cos^2 y=sinh^2 x when z=x+iy

$p r o v e t h a t$ $∣ \frac{e^{z} - e^{- z}}{2} ∣^{2} + {c o s}^{2} y = {s i n h}^{2} x w h e n z = x + i y$

Question Number 88261 Answers: 1 Comments: 0

Question Number 88253 Answers: 0 Comments: 0

∫ ((ln(x^2 +1) dx)/(x+1))

$\int \frac{\ln (x^{2} + 1) d x}{x + 1}$

Question Number 88252 Answers: 0 Comments: 0

Question Number 88251 Answers: 0 Comments: 0

Question Number 88245 Answers: 2 Comments: 0

Question Number 88240 Answers: 1 Comments: 3

Question Number 88239 Answers: 0 Comments: 0

Question Number 88238 Answers: 1 Comments: 0

solve (3x^5 y^4 +4y)dx+(2x^6 y^3 +3x)dy=0

$s o l v e$ $(3 x^{5} y^{4} + 4 y) d x + (2 x^{6} y^{3} + 3 x) d y = 0$

Question Number 88236 Answers: 1 Comments: 0

Evaluate ∫(((27)/(x^3 −6)))^(1/3) dx

$Evaluate \int \sqrt[3]{\frac{27}{x^{3} - 6}} d x$

Question Number 88235 Answers: 0 Comments: 1

find a maclaurine series solution to the differential equation up to the term in x^4 . (dy/dx) − x = xy if y = 1 when x = 0.

$find a maclaurine series solution to the differential equation$ $up to the term in x^{4} .$ $\frac{d y}{d x} - x = x y if y = 1 when x = 0 .$

Question Number 88232 Answers: 0 Comments: 0

Pg 1196 Pg 1197 Pg 1198 Pg 1199 Pg 1200 Pg 1201 Pg 1202 Pg 1203 Pg 1204 Pg 1205

Contact: info@tinkutara.com