Question and Answers Forum

AllQuestion and Answers: Page 1200

Question Number 96715 Answers: 1 Comments: 0

find real solution of equation x^5 +x^4 +1 = 0

$$\mathrm{find}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{equation} \\ $$$${x}^{\mathrm{5}} +{x}^{\mathrm{4}} +\mathrm{1}\:=\:\mathrm{0} \\ $$

Question Number 96713 Answers: 1 Comments: 0

y^2 (d^2 y/dx^2 )=(dy/dx)

$${y}^{\mathrm{2}} \:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{dy}}{{dx}} \\ $$

Question Number 96712 Answers: 1 Comments: 0

Question Number 96705 Answers: 1 Comments: 0

∫ ln((√(1−x))+(√(1+x))) dx = ?

$$\int\:\mathrm{ln}\left(\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{1}+\mathrm{x}}\right)\:\mathrm{dx}\:=\:? \\ $$

Question Number 96699 Answers: 0 Comments: 2

∫ ((tan^3 (ln x))/x) dx = ??

$$\int\:\frac{\mathrm{tan}^{\mathrm{3}} \left(\mathrm{ln}\:{x}\right)}{{x}}\:{dx}\:=\:?? \\ $$

Question Number 96693 Answers: 1 Comments: 0

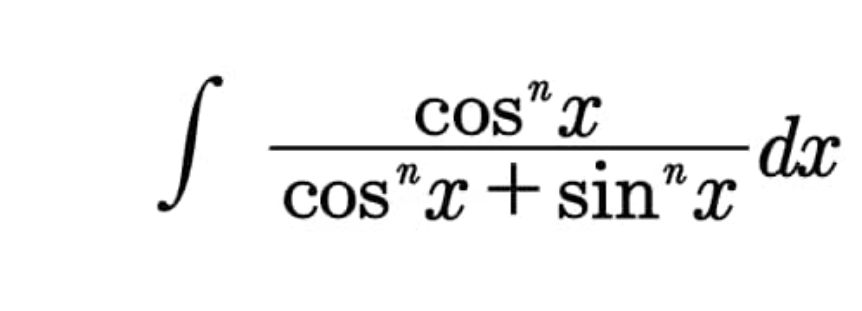
Question Number 96685 Answers: 1 Comments: 0

lim_(ω→∞) 20log(√(1+((ω/(100)))^2 ))

$$\underset{\omega\rightarrow\infty} {\mathrm{lim}20log}\sqrt{\mathrm{1}+\left(\frac{\omega}{\mathrm{100}}\right)^{\mathrm{2}} } \\ $$

Question Number 96684 Answers: 2 Comments: 0

lim_(n→+∞) Σ_(k=1) ^n ((n+k)/(n^2 +k^2 )) {Reimann′s integral may help}

$$\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}+\mathrm{k}}{\mathrm{n}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} } \\ $$$$\left\{\mathrm{Reimann}'\mathrm{s}\:\:\mathrm{integral}\:\:\mathrm{may}\:\:\mathrm{help}\right\} \\ $$

Question Number 96682 Answers: 1 Comments: 4

Question Number 96679 Answers: 1 Comments: 0

I=∫_0 ^1 ((1−x)/(x^2 +(x^2 +1)^2 ))dx find tan(I)+sec(I)

$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{{x}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${find}\:\:\:\:{tan}\left({I}\right)+{sec}\left({I}\right) \\ $$

Question Number 96672 Answers: 0 Comments: 1

Evaluate : ∫ ((log_x a)/x) dx

$${Evaluate}\:: \\ $$$$\int\:\frac{{log}_{{x}} {a}}{{x}}\:{dx} \\ $$

Question Number 96671 Answers: 1 Comments: 0

Question Number 96669 Answers: 2 Comments: 0

find minimum value f(x) = (√(x^2 +9))+(√(x^2 −30x+250))

$$\mathrm{find}\:\mathrm{minimum}\:\mathrm{value} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{30x}+\mathrm{250}} \\ $$

Question Number 96667 Answers: 2 Comments: 0

Prove that Σ_(k=1) ^∞ (1/k^2 )=(π^2 /6)

$$\mathcal{P}\mathrm{rove}\:\:\mathrm{that}\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Question Number 96660 Answers: 1 Comments: 0

calculate L( e^(−2x) cos(πx)) L laplace transform

$$\mathrm{calculate}\:\mathrm{L}\left(\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{cos}\left(\pi\mathrm{x}\right)\right)\:\:\:\mathrm{L}\:\mathrm{laplace}\:\mathrm{transform} \\ $$

Question Number 96659 Answers: 1 Comments: 0

find L (((sh(3x))/x)) L laplace transform

$$\mathrm{find}\:\mathrm{L}\:\left(\frac{\mathrm{sh}\left(\mathrm{3x}\right)}{\mathrm{x}}\right)\:\mathrm{L}\:\mathrm{laplace}\:\mathrm{transform} \\ $$

Question Number 96658 Answers: 1 Comments: 0

determine L(e^(−x^2 −x) ) with L laplace transform

$$\mathrm{determine}\:\mathrm{L}\left(\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{x}} \right)\:\:\:\mathrm{with}\:\mathrm{L}\:\mathrm{laplace}\:\mathrm{transform} \\ $$

Question Number 96657 Answers: 2 Comments: 0

f(x) =e^(−x) , 2π periodic developp f at fourier serie

$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{x}} \:,\:\:\mathrm{2}\pi\:\mathrm{periodic}\:\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 96656 Answers: 1 Comments: 0

let g(x) =(2/(cosx)) developp f at fourier serie

$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{cosx}}\:\:\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 96655 Answers: 1 Comments: 0

let f(x) =ln(2+cosx) developp f at fourier serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{2}+\mathrm{cosx}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 96652 Answers: 1 Comments: 0

∫ ((xcos x−sin x)/(x^2 +sin^2 x)) dx

$$\int\:\frac{{x}\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$

Question Number 96650 Answers: 1 Comments: 0

solve 2 ((2y−1))^(1/(3 )) = y^3 +1

$$\mathrm{solve}\:\mathrm{2}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2y}−\mathrm{1}}\:=\:\mathrm{y}^{\mathrm{3}} +\mathrm{1} \\ $$

Question Number 96637 Answers: 0 Comments: 1

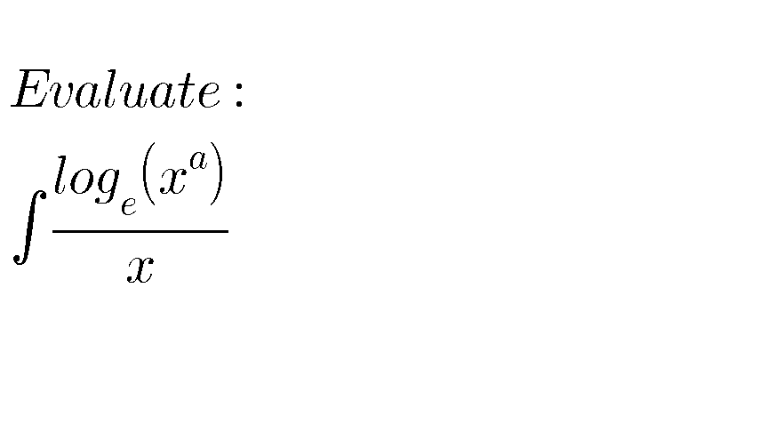
Question Number 96636 Answers: 2 Comments: 1

Question Number 96617 Answers: 0 Comments: 2

Given matrix A [((a c)),((b d)) ]and B ((x),(y_ ) ). Determinate A×B and B×A.

$${Given}\:{matrix}\:{A}\begin{bmatrix}{{a}\:\:\:\:\:{c}}\\{{b}\:\:\:\:\:{d}}\end{bmatrix}{and}\:{B}\begin{pmatrix}{{x}}\\{{y}_{} }\end{pmatrix}. \\ $$$${Determinate}\:{A}×{B}\:{and}\:{B}×{A}. \\ $$

Question Number 96616 Answers: 1 Comments: 0

Pg 1195 Pg 1196 Pg 1197 Pg 1198 Pg 1199 Pg 1200 Pg 1201 Pg 1202 Pg 1203 Pg 1204

Contact: info@tinkutara.com