
AllQuestion and Answers: Page 1199
Question Number 96834 Answers: 2 Comments: 1
Question Number 96829 Answers: 0 Comments: 1
Question Number 96826 Answers: 1 Comments: 0
Question Number 96823 Answers: 2 Comments: 2
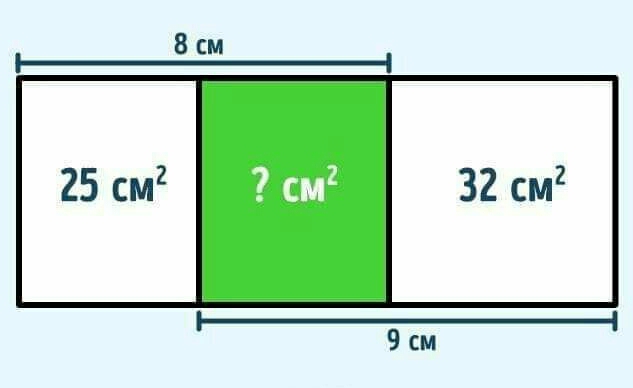
Question Number 96821 Answers: 3 Comments: 0
Question Number 96817 Answers: 1 Comments: 2

Question Number 96815 Answers: 1 Comments: 0
Question Number 96811 Answers: 1 Comments: 0
Question Number 96792 Answers: 1 Comments: 12
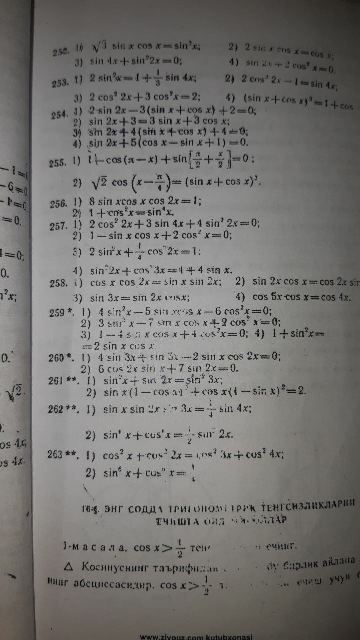
Question Number 96785 Answers: 1 Comments: 0

Question Number 96784 Answers: 1 Comments: 0

Question Number 96782 Answers: 3 Comments: 1
Question Number 96780 Answers: 0 Comments: 5

Question Number 96773 Answers: 1 Comments: 0
$$\mathrm{solve}\:\mathrm{y}^{''} −\mathrm{y}\:=\frac{\mathrm{sinx}}{\mathrm{x}} \\ $$
Question Number 96772 Answers: 2 Comments: 0
Question Number 96771 Answers: 1 Comments: 0
Question Number 96766 Answers: 1 Comments: 0
Question Number 96764 Answers: 1 Comments: 5
Question Number 96763 Answers: 2 Comments: 0
Question Number 96761 Answers: 0 Comments: 0
Question Number 96758 Answers: 0 Comments: 1
Question Number 96749 Answers: 1 Comments: 0
Question Number 96748 Answers: 0 Comments: 1
$$\mathrm{nobody}\:\mathrm{tried}\:\mathrm{question}\:\mathrm{94184}... \\ $$
Question Number 96730 Answers: 1 Comments: 0
Question Number 96729 Answers: 2 Comments: 1
Question Number 96746 Answers: 3 Comments: 2
Pg 1194 Pg 1195 Pg 1196 Pg 1197 Pg 1198 Pg 1199 Pg 1200 Pg 1201 Pg 1202 Pg 1203
