
AllQuestion and Answers: Page 1194
Question Number 97866 Answers: 5 Comments: 4

Question Number 97858 Answers: 1 Comments: 1
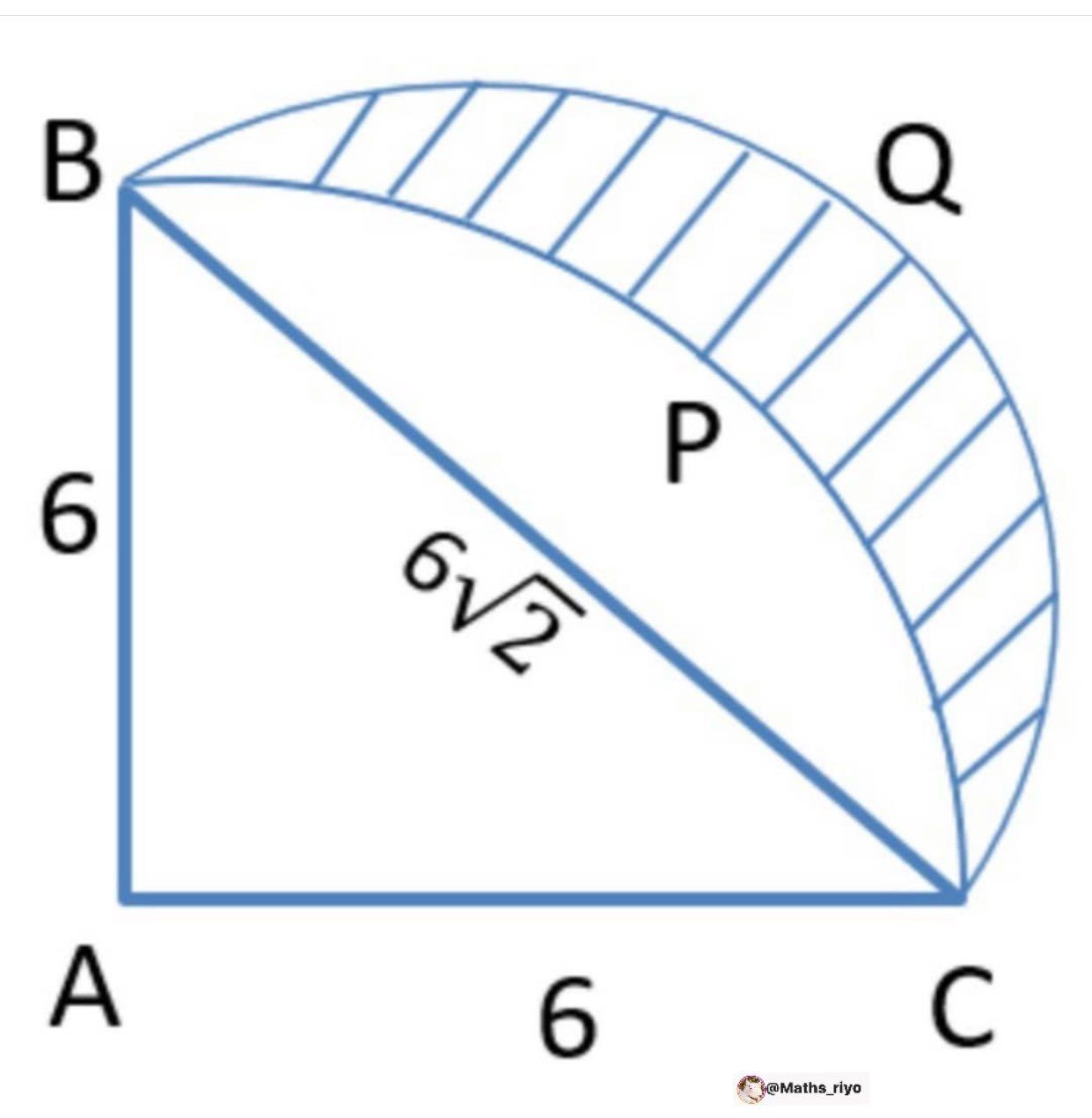
Question Number 97847 Answers: 1 Comments: 0
Question Number 97840 Answers: 0 Comments: 1
Question Number 97839 Answers: 3 Comments: 1
Question Number 97833 Answers: 0 Comments: 10
Question Number 97827 Answers: 0 Comments: 1

Question Number 97823 Answers: 4 Comments: 2
Question Number 97818 Answers: 1 Comments: 0
Question Number 97808 Answers: 0 Comments: 1

Question Number 97807 Answers: 0 Comments: 0
Question Number 97803 Answers: 1 Comments: 0
Question Number 97800 Answers: 3 Comments: 0
Question Number 97799 Answers: 0 Comments: 1
Question Number 97798 Answers: 0 Comments: 0
$$\mathrm{solve}\:\mathrm{y}''−\mathrm{y}\:=\mathrm{xsin}\left(\mathrm{2x}\right) \\ $$
Question Number 97797 Answers: 3 Comments: 0
$$\mathrm{solve}\:\mathrm{y}^{''} \:−\mathrm{y}\:=\:\mathrm{x} \\ $$
Question Number 97795 Answers: 1 Comments: 0
Question Number 97794 Answers: 1 Comments: 3
$$\mathrm{solve}\:\mathrm{y}^{''} \:+\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$
Question Number 97784 Answers: 1 Comments: 0
Question Number 97782 Answers: 2 Comments: 1
$${Evaluate}: \\ $$$$\int\:\frac{{sinx}}{\mathrm{1}\:+{sin}^{\mathrm{2}} {x}}{dx} \\ $$
Question Number 97781 Answers: 1 Comments: 0
Question Number 97779 Answers: 0 Comments: 1

Question Number 97775 Answers: 3 Comments: 2

Question Number 97759 Answers: 1 Comments: 0
Question Number 97752 Answers: 1 Comments: 4

Question Number 97751 Answers: 2 Comments: 3
Pg 1189 Pg 1190 Pg 1191 Pg 1192 Pg 1193 Pg 1194 Pg 1195 Pg 1196 Pg 1197 Pg 1198
