Question and Answers Forum

AllQuestion and Answers: Page 1192

Question Number 98130 Answers: 0 Comments: 0

Question Number 98119 Answers: 0 Comments: 1

Find the shortest distance between the skew lines ((x−3)/3) = ((8−y)/1) = ((z−3)/1) and ((x+3)/(−3)) = ((y+7)/2) = ((z−6)/4) .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the} \\ $$$$\mathrm{skew}\:\mathrm{lines}\:\frac{\mathrm{x}−\mathrm{3}}{\mathrm{3}}\:=\:\frac{\mathrm{8}−\mathrm{y}}{\mathrm{1}}\:=\:\frac{\mathrm{z}−\mathrm{3}}{\mathrm{1}}\:\mathrm{and}\: \\ $$$$\frac{\mathrm{x}+\mathrm{3}}{−\mathrm{3}}\:=\:\frac{\mathrm{y}+\mathrm{7}}{\mathrm{2}}\:=\:\frac{\mathrm{z}−\mathrm{6}}{\mathrm{4}}\:. \\ $$

Question Number 98118 Answers: 1 Comments: 0

calculate Σ_(n=1) ^∞ (ξ(2n)−1)x^(2n) ξ(x)=Σ_(n=1) ^∞ (1/n^x )

$$\mathrm{calculate}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(\xi\left(\mathrm{2n}\right)−\mathrm{1}\right)\mathrm{x}^{\mathrm{2n}} \\ $$$$\xi\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{x}} } \\ $$

Question Number 98116 Answers: 0 Comments: 0

prove the compact form of multivariable Taylor series (T∗B)=Σ_(n=1,n=2..n_d =0) ^∞ ((Π_(i=0) ^n_d (x_i −d_i ))/(Π_(i=0) ^n_d (n_i )!)) Π_(i=0) ^n_d (∂/∂x_i )f

$${prove}\:{the}\:{compact}\:{form}\:{of}\:{multivariable} \\ $$$${Taylor}\:{series} \\ $$$$ \\ $$$$\left({T}\ast{B}\right)=\underset{{n}=\mathrm{1},{n}=\mathrm{2}..{n}_{{d}} =\mathrm{0}} {\overset{\infty} {\sum}}\frac{\prod_{\mathrm{i}=\mathrm{0}} ^{{n}_{{d}} } \left({x}_{\mathrm{i}} −{d}_{\mathrm{i}} \right)}{\prod_{\mathrm{i}=\mathrm{0}} ^{{n}_{{d}} } \left({n}_{\mathrm{i}} \right)!}\:\underset{\mathrm{i}=\mathrm{0}} {\overset{{n}_{{d}} } {\prod}}\frac{\partial}{\partial{x}_{\mathrm{i}} }{f} \\ $$

Question Number 98114 Answers: 1 Comments: 0

1 lim_(x→∞) ^3 (√(5x^3 )) = ? 2 lim_(x→∞) (1 + (n/(x + 𝛂)))^x ;𝛂 is constant

$$\mathrm{1}\:\:\:\underset{\boldsymbol{{x}}\rightarrow\infty} {\boldsymbol{{lim}}}\:^{\mathrm{3}} \sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{3}} }\:=\:? \\ $$$$\mathrm{2}\:\:\underset{\boldsymbol{{x}}\rightarrow\infty} {\boldsymbol{{lim}}}\:\left(\mathrm{1}\:+\:\frac{\boldsymbol{{n}}}{\boldsymbol{{x}}\:+\:\boldsymbol{\alpha}}\right)^{\boldsymbol{{x}}} ;\boldsymbol{\alpha}\:\boldsymbol{{is}}\:\boldsymbol{{constant}} \\ $$

Question Number 98112 Answers: 1 Comments: 0

Σ_(n=1) ^∞ (1/2^n^2 )

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}^{\mathrm{2}} } } \\ $$

Question Number 98106 Answers: 2 Comments: 0

y′′+y = cos 3x−2sin 3x

$$\mathrm{y}''+\mathrm{y}\:=\:\mathrm{cos}\:\mathrm{3x}−\mathrm{2sin}\:\mathrm{3x} \\ $$

Question Number 98105 Answers: 2 Comments: 0

calculate ∫_3 ^(+∞) (((x+1)dx)/((x−2)^2 ( 2x+3)^3 ))

$$\mathrm{calculate}\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \left(\:\mathrm{2x}+\mathrm{3}\right)^{\mathrm{3}} } \\ $$

Question Number 98104 Answers: 5 Comments: 1

Determine the value of x+y if { ((x^3 +y^3 =1)),(((x+y)(x+1)(y+1)=2)) :}

$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}+\mathrm{y}\: \\ $$$$\mathrm{if}\:\begin{cases}{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} =\mathrm{1}}\\{\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{y}+\mathrm{1}\right)=\mathrm{2}}\end{cases} \\ $$$$ \\ $$

Question Number 98098 Answers: 3 Comments: 0

what is the length of the chord cut off by y = 2x+1 from circle x^2 +y^2 =2

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{cut} \\ $$$$\mathrm{off}\:\mathrm{by}\:\mathrm{y}\:=\:\mathrm{2x}+\mathrm{1}\:\mathrm{from}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2} \\ $$

Question Number 98096 Answers: 1 Comments: 0

Question Number 98091 Answers: 1 Comments: 0

what is number of positive integral solutions of 10xy+7x+3y = 2077829313

$$\mathrm{what}\:\mathrm{is}\:\mathrm{number}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integral}\: \\ $$$$\mathrm{solutions}\:\mathrm{of}\:\mathrm{10xy}+\mathrm{7x}+\mathrm{3y}\:=\:\mathrm{2077829313} \\ $$

Question Number 98087 Answers: 1 Comments: 0

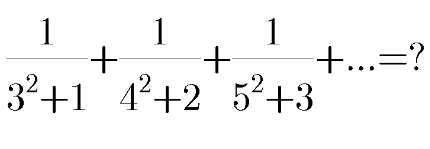
Question Number 98077 Answers: 0 Comments: 4

Question Number 98073 Answers: 1 Comments: 2

solve (√(6−x)) = 6−x^2

$$\mathrm{solve}\:\sqrt{\mathrm{6}−\mathrm{x}}\:=\:\mathrm{6}−\mathrm{x}^{\mathrm{2}} \\ $$

Question Number 98067 Answers: 2 Comments: 0

Question Number 98060 Answers: 1 Comments: 0

show that Σ_(n=1) ^∞ arctan((2/n^2 ))=((3π)/4)

$${show}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{arctan}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\right)=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$

Question Number 98058 Answers: 1 Comments: 0

If the equation x^2 −cx+d=0 has roots equal to the fourth powers of the roots of x^2 +ax+b=0, where a^2 >4b then the roots of x^2 −4bx+2b^2 −c=0 will be

$$\mathrm{If}\:\mathrm{the}\:\mathrm{equation}\:{x}^{\mathrm{2}} −{cx}+{d}=\mathrm{0}\:\mathrm{has}\:\mathrm{roots} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{fourth}\:\mathrm{powers}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots} \\ $$$$\mathrm{of}\:{x}^{\mathrm{2}} +{ax}+{b}=\mathrm{0},\:\mathrm{where}\:{a}^{\mathrm{2}} >\mathrm{4}{b}\:\mathrm{then}\:\mathrm{the} \\ $$$$\mathrm{roots}\:\mathrm{of}\:{x}^{\mathrm{2}} −\mathrm{4}{bx}+\mathrm{2}{b}^{\mathrm{2}} −{c}=\mathrm{0}\:\mathrm{will}\:\mathrm{be} \\ $$

Question Number 98057 Answers: 2 Comments: 0

The number of real solutions of 3^x +4^x =5^x is ____.

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\mathrm{3}^{{x}} +\mathrm{4}^{{x}} =\mathrm{5}^{{x}} \:\mathrm{is}\:\_\_\_\_. \\ $$

Question Number 98056 Answers: 0 Comments: 3

The number of real roots of the quadratic equation (x−4)^2 +(x−5)^2 +(x−6)^2 =0 is

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic} \\ $$$$\mathrm{equation}\:\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({x}−\mathrm{6}\right)^{\mathrm{2}} =\mathrm{0}\:\mathrm{is} \\ $$

Question Number 98039 Answers: 1 Comments: 0

10000×((10)/(100))×((20)/(100))×((30)/(100))=

$$\mathrm{10000}×\frac{\mathrm{10}}{\mathrm{100}}×\frac{\mathrm{20}}{\mathrm{100}}×\frac{\mathrm{30}}{\mathrm{100}}= \\ $$$$ \\ $$

Question Number 98035 Answers: 0 Comments: 4

Question Number 98030 Answers: 0 Comments: 1

Question Number 98027 Answers: 0 Comments: 1

One card is randomly selected from a pack of 52 playing cards. Determine the probability that is a picture card.

$$\mathrm{One}\:\mathrm{card}\:\mathrm{is}\:\mathrm{randomly}\:\mathrm{selected} \\ $$$$\mathrm{from}\:\mathrm{a}\:\mathrm{pack}\:\mathrm{of}\:\mathrm{52}\:\mathrm{playing}\:\mathrm{cards}. \\ $$$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\: \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{picture}\:\mathrm{card}.\: \\ $$

Question Number 98022 Answers: 1 Comments: 0

Derive the relation between an Arithmetic Mean and a Geometric Mean ((x_1 x_2 ...x_n ))^(1/n) ≤((x_1 +x_2 +∙∙∙+x_n )/n) ∀n∈N^∗ , ∀(x_1 ,x_2 ,...x_n )∈(R_+ ^∗ )^n

$$\mathcal{D}\mathrm{erive}\:\mathrm{the}\:\mathrm{relation}\:\mathrm{between}\:\mathrm{an}\:\mathcal{A}\mathrm{rithmetic}\:\mathcal{M}\mathrm{ean} \\ $$$$\mathrm{and}\:\mathrm{a}\:\mathcal{G}\mathrm{eometric}\:\mathcal{M}\mathrm{ean} \\ $$$$\sqrt[{\mathrm{n}}]{\mathrm{x}_{\mathrm{1}} \mathrm{x}_{\mathrm{2}} ...\mathrm{x}_{\mathrm{n}} }\leqslant\frac{\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{x}_{\mathrm{n}} }{\mathrm{n}}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} ,\:\forall\left(\mathrm{x}_{\mathrm{1}} ,\mathrm{x}_{\mathrm{2}} ,...\mathrm{x}_{\mathrm{n}} \right)\in\left(\mathbb{R}_{+} ^{\ast} \right)^{\mathrm{n}} \\ $$

Question Number 98020 Answers: 1 Comments: 0

What is the area of the region bounded by x^2 +y^2 ≤ 9 ; x+y ≤ 3 and y ≤ x

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{region}\:\mathrm{bounded} \\ $$$$\mathrm{by}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:\leqslant\:\mathrm{9}\:;\:\mathrm{x}+\mathrm{y}\:\leqslant\:\mathrm{3}\:\mathrm{and}\:\mathrm{y}\:\leqslant\:\mathrm{x}\: \\ $$

Pg 1187 Pg 1188 Pg 1189 Pg 1190 Pg 1191 Pg 1192 Pg 1193 Pg 1194 Pg 1195 Pg 1196

Contact: [email protected]