
AllQuestion and Answers: Page 1190
Question Number 97928 Answers: 1 Comments: 0
Question Number 97922 Answers: 1 Comments: 0
Question Number 97918 Answers: 0 Comments: 1
Question Number 97920 Answers: 0 Comments: 4

Question Number 97919 Answers: 1 Comments: 2
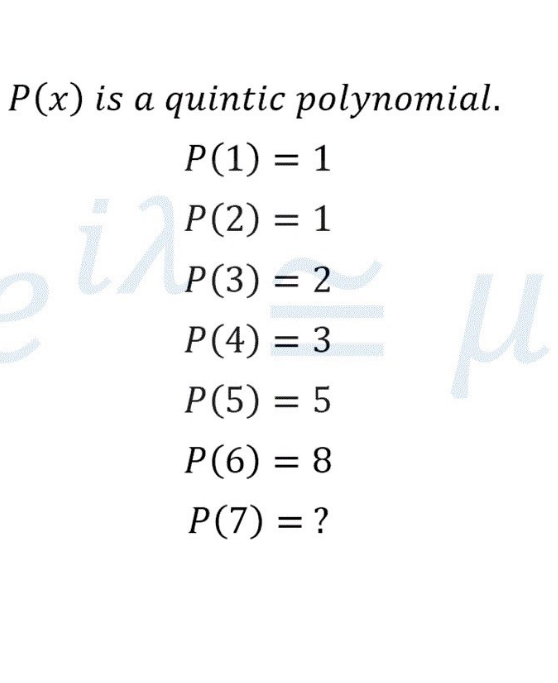
Question Number 97901 Answers: 2 Comments: 2
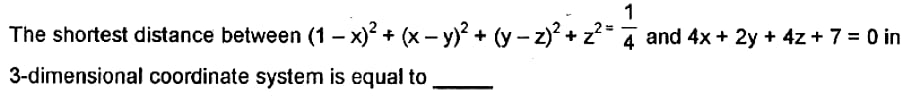
Question Number 97888 Answers: 1 Comments: 2
Question Number 97891 Answers: 0 Comments: 6
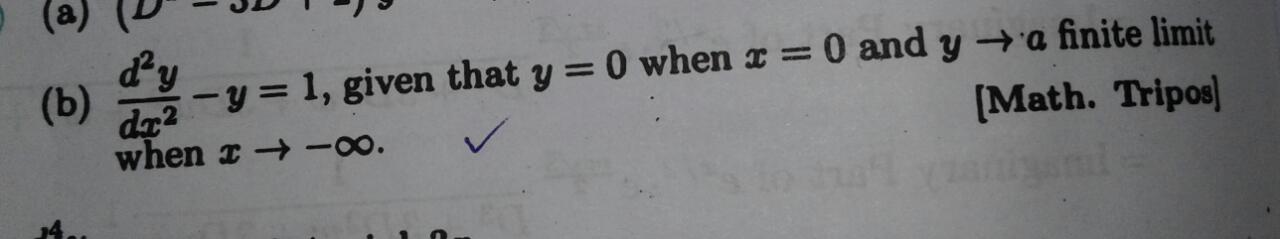
Question Number 97885 Answers: 2 Comments: 2
Question Number 97868 Answers: 2 Comments: 0
$$\mathrm{3y}'\:=\:\mathrm{2x}+\mathrm{y}−\mathrm{1}\: \\ $$
Question Number 97866 Answers: 5 Comments: 4

Question Number 97858 Answers: 1 Comments: 1
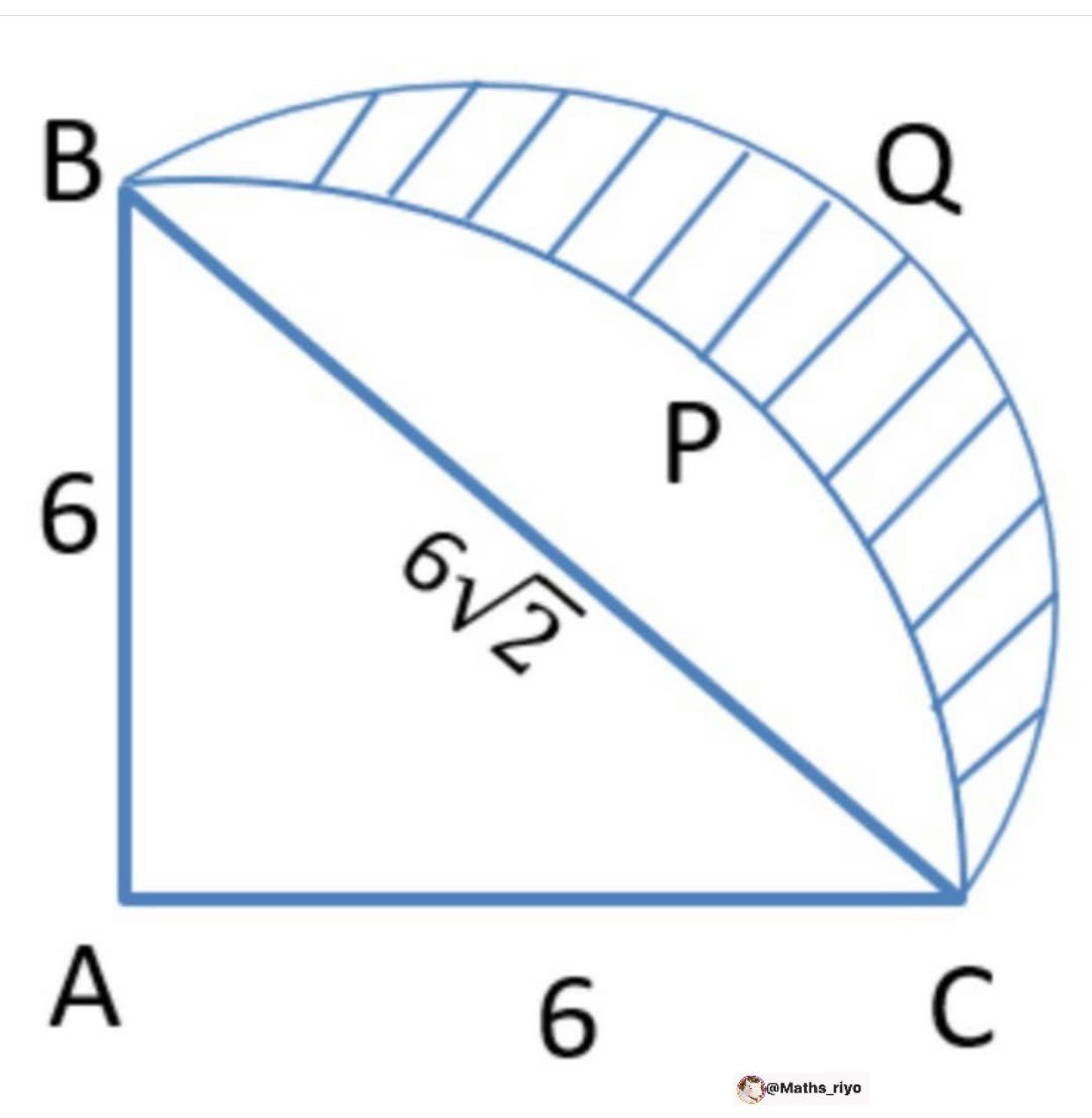
Question Number 97847 Answers: 1 Comments: 0
Question Number 97840 Answers: 0 Comments: 1
Question Number 97839 Answers: 3 Comments: 1
Question Number 97833 Answers: 0 Comments: 10
Question Number 97827 Answers: 0 Comments: 1

Question Number 97823 Answers: 4 Comments: 2
Question Number 97818 Answers: 1 Comments: 0
Question Number 97808 Answers: 0 Comments: 1

Question Number 97807 Answers: 0 Comments: 0
Question Number 97803 Answers: 1 Comments: 0
Question Number 97800 Answers: 3 Comments: 0
Question Number 97799 Answers: 0 Comments: 1
Question Number 97798 Answers: 0 Comments: 0
$$\mathrm{solve}\:\mathrm{y}''−\mathrm{y}\:=\mathrm{xsin}\left(\mathrm{2x}\right) \\ $$
Question Number 97797 Answers: 3 Comments: 0
$$\mathrm{solve}\:\mathrm{y}^{''} \:−\mathrm{y}\:=\:\mathrm{x} \\ $$
Pg 1185 Pg 1186 Pg 1187 Pg 1188 Pg 1189 Pg 1190 Pg 1191 Pg 1192 Pg 1193 Pg 1194
