
AllQuestion and Answers: Page 1189
Question Number 98443 Answers: 1 Comments: 0
Question Number 98434 Answers: 0 Comments: 5
Question Number 98430 Answers: 1 Comments: 0
Question Number 98429 Answers: 1 Comments: 0
Question Number 98416 Answers: 3 Comments: 0

Question Number 98408 Answers: 1 Comments: 0
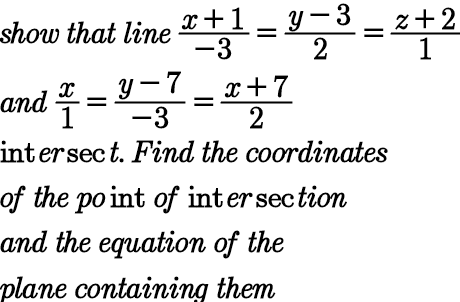
Question Number 98405 Answers: 1 Comments: 0

Question Number 98406 Answers: 0 Comments: 0
Question Number 98398 Answers: 4 Comments: 2
Question Number 98428 Answers: 1 Comments: 0
Question Number 98426 Answers: 2 Comments: 0
Question Number 98425 Answers: 0 Comments: 0
Question Number 98424 Answers: 1 Comments: 0
Question Number 98423 Answers: 1 Comments: 0
Question Number 98382 Answers: 0 Comments: 2
Question Number 98380 Answers: 3 Comments: 0
Question Number 98369 Answers: 2 Comments: 0
Question Number 98368 Answers: 1 Comments: 0
Question Number 98367 Answers: 1 Comments: 2
Question Number 98355 Answers: 1 Comments: 1

Question Number 98342 Answers: 1 Comments: 2

Question Number 98338 Answers: 2 Comments: 0
$$\int{cos}\left({x}^{\mathrm{18}} \right)\:{dx} \\ $$$$ \\ $$
Question Number 98325 Answers: 1 Comments: 0
Question Number 98320 Answers: 1 Comments: 0

Question Number 98311 Answers: 1 Comments: 0
Question Number 98310 Answers: 0 Comments: 0
Pg 1184 Pg 1185 Pg 1186 Pg 1187 Pg 1188 Pg 1189 Pg 1190 Pg 1191 Pg 1192 Pg 1193
