
AllQuestion and Answers: Page 1188
Question Number 98539 Answers: 2 Comments: 0
Question Number 98537 Answers: 1 Comments: 1

Question Number 98535 Answers: 0 Comments: 0
Question Number 98531 Answers: 0 Comments: 0

Question Number 98528 Answers: 0 Comments: 2

Question Number 98521 Answers: 1 Comments: 0

Question Number 98520 Answers: 1 Comments: 0
Question Number 98516 Answers: 2 Comments: 2
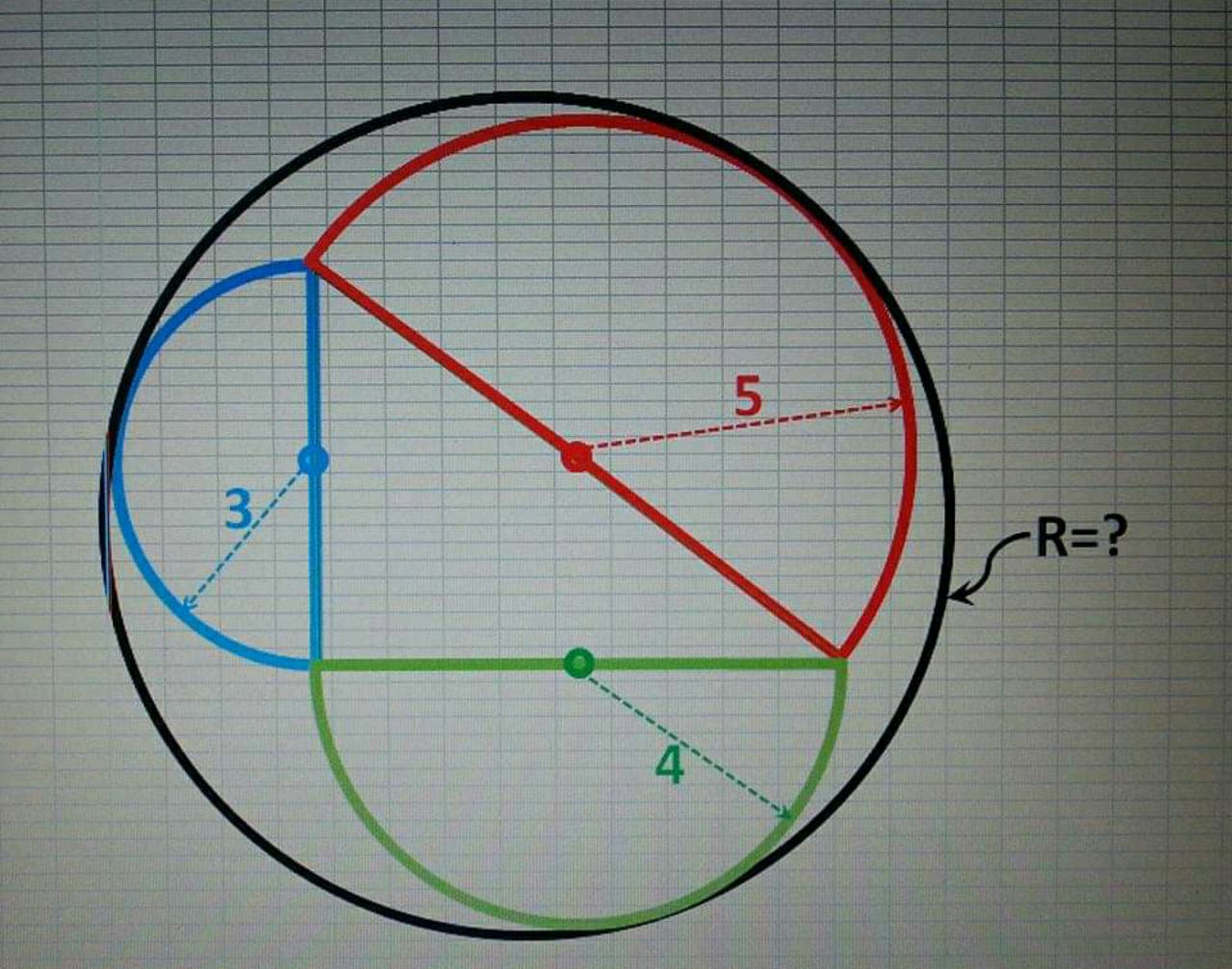
Question Number 98506 Answers: 0 Comments: 1
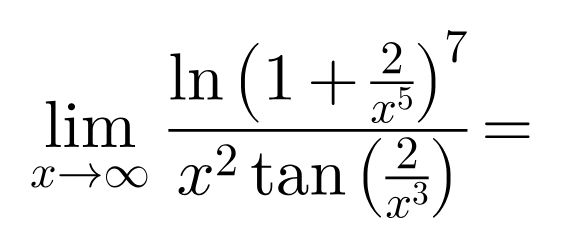
Question Number 98470 Answers: 0 Comments: 0
Question Number 98468 Answers: 2 Comments: 10

Question Number 98464 Answers: 1 Comments: 0
Question Number 98463 Answers: 1 Comments: 0
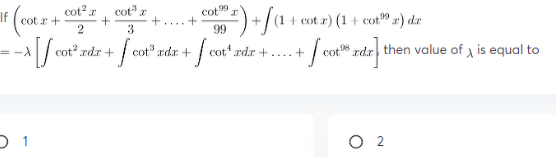
Question Number 98461 Answers: 3 Comments: 1
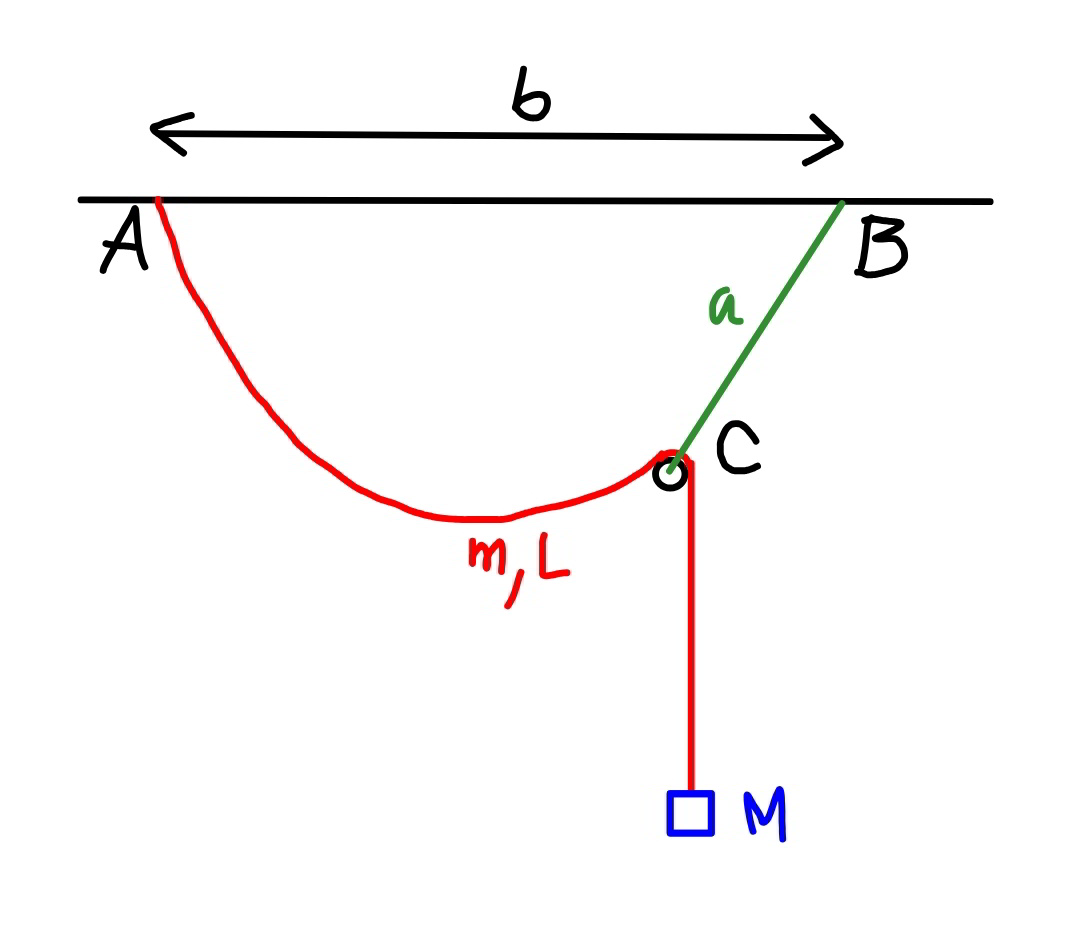
Question Number 98453 Answers: 0 Comments: 2
Question Number 98613 Answers: 0 Comments: 0
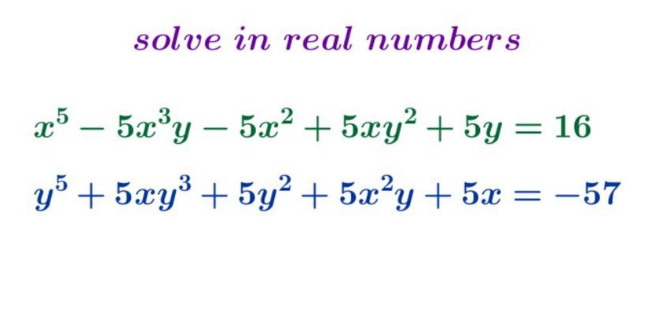
Question Number 98450 Answers: 0 Comments: 1
Question Number 98448 Answers: 1 Comments: 5
Question Number 98445 Answers: 2 Comments: 0
Question Number 98444 Answers: 1 Comments: 0
Question Number 98443 Answers: 1 Comments: 0
Question Number 98434 Answers: 0 Comments: 5
Question Number 98430 Answers: 1 Comments: 0
Question Number 98429 Answers: 1 Comments: 0
Question Number 98416 Answers: 3 Comments: 0

Question Number 98408 Answers: 1 Comments: 0
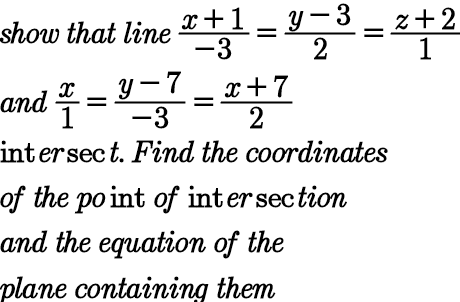
Pg 1183 Pg 1184 Pg 1185 Pg 1186 Pg 1187 Pg 1188 Pg 1189 Pg 1190 Pg 1191 Pg 1192
