Question and Answers Forum

AllQuestion and Answers: Page 1187

Question Number 98208 Answers: 0 Comments: 2

suppose a force given as F_1 = 24 N and F_2 = 50 N act through points AB and AC where OA = 2i +3j , OB = 5i + 6j and OC = 7i + 8j (a) find in vector notation F_1 and F_2 then find thier resultant.

$$\mathrm{suppose}\:\mathrm{a}\:\mathrm{force}\:\mathrm{given}\:\mathrm{as}\:{F}_{\mathrm{1}} \:=\:\mathrm{24}\:{N}\:\mathrm{and}\:{F}_{\mathrm{2}} \:=\:\mathrm{50}\:{N}\:\mathrm{act}\:\mathrm{through}\: \\ $$$$\mathrm{points}\:{AB}\:\mathrm{and}\:{AC}\:\mathrm{where}\:\:{OA}\:=\:\mathrm{2}{i}\:+\mathrm{3}{j}\:,\:{OB}\:=\:\mathrm{5}{i}\:+\:\mathrm{6}{j}\:\:\mathrm{and}\: \\ $$$${OC}\:=\:\mathrm{7}{i}\:+\:\mathrm{8}{j} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{find}\:\mathrm{in}\:\mathrm{vector}\:\mathrm{notation}\:{F}_{\mathrm{1}} \:\mathrm{and}\:{F}_{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{thier}\:\mathrm{resultant}. \\ $$

Question Number 98213 Answers: 2 Comments: 1

Question Number 98205 Answers: 1 Comments: 0

Find the nth term of the sequence {a_n } such that a_1 = 1, a_(n + 1) = (1/2)a_n + ((n^2 − 2n − 1)/(n^2 (n + 1)^2 )) (n = 1, 2, 3, ...)

Question Number 98201 Answers: 1 Comments: 0

Question Number 98286 Answers: 0 Comments: 0

justify: lim_(x→+∞) Σ_(k≥1) (((k−1)! sin(x−(π/2)k))/x^k )=(π/2)

$${justify}: \\ $$$$\underset{{x}\rightarrow+\infty} {{lim}}\:\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left({k}−\mathrm{1}\right)!\:{sin}\left({x}−\frac{\pi}{\mathrm{2}}{k}\right)}{{x}^{{k}} }=\frac{\pi}{\mathrm{2}} \\ $$

Question Number 98192 Answers: 2 Comments: 1

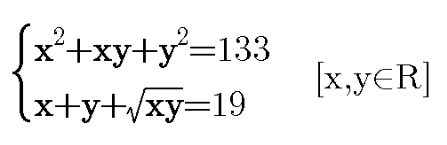
Question Number 98191 Answers: 2 Comments: 0

for what value of :{x∣ 0<x<2𝛑}: 4cosec^2 x−9=cotx

$$\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{what}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\::\left\{\boldsymbol{\mathrm{x}}\mid\:\mathrm{0}<\boldsymbol{\mathrm{x}}<\mathrm{2}\boldsymbol{\pi}\right\}:\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{4}\boldsymbol{\mathrm{cosec}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}−\mathrm{9}=\boldsymbol{\mathrm{cotx}} \\ $$

Question Number 98190 Answers: 1 Comments: 0

Question Number 98189 Answers: 1 Comments: 0

let ξ(x) =Σ_(n=1) ^∞ (1/n^x ) calculate lim_(x→1^+ ) (x−1)ξ(x)

$$\mathrm{let}\:\xi\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{x}} } \\ $$$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\:\left(\mathrm{x}−\mathrm{1}\right)\xi\left(\mathrm{x}\right) \\ $$

Question Number 98188 Answers: 1 Comments: 0

let f(x) =((arctan(2x))/(x+3)) 1) calculate f^((n)) (x) snd f^((n)) (0) 2) developp f at integr serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{arctan}\left(\mathrm{2x}\right)}{\mathrm{x}+\mathrm{3}} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\mathrm{snd}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$

Question Number 98187 Answers: 3 Comments: 0

find arctan(x)+arctany at form of arctan

$$\mathrm{find}\:\mathrm{arctan}\left(\mathrm{x}\right)+\mathrm{arctany}\:\:\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{arctan} \\ $$

Question Number 98186 Answers: 0 Comments: 0

solve xy^((3)) +x^2 y^((2)) +x^3 y^((1)) +x^4 y =e^(−2x)

$$\mathrm{solve}\:\mathrm{xy}^{\left(\mathrm{3}\right)} \:+\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\left(\mathrm{2}\right)} \:+\mathrm{x}^{\mathrm{3}} \mathrm{y}^{\left(\mathrm{1}\right)} \:+\mathrm{x}^{\mathrm{4}} \mathrm{y}\:=\mathrm{e}^{−\mathrm{2x}} \\ $$

Question Number 98185 Answers: 1 Comments: 0

developp at fourier serie g(x) =(2/(3+sin^2 x))

$$\mathrm{developp}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$

Question Number 98184 Answers: 1 Comments: 0

let f(x) =∫_0 ^∞ ((cos(xt))/((t^2 +4)^2 ))dt find ∫_0 ^1 f(x)dx

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{xt}\right)}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\mathrm{dt}\:\:\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Question Number 98183 Answers: 0 Comments: 0

solve xy^(′′) −(3/(x+1))y^′ =xsin(x)

$$\mathrm{solve}\:\mathrm{xy}^{''} \:−\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}\mathrm{y}^{'} \:=\mathrm{xsin}\left(\mathrm{x}\right) \\ $$

Question Number 98182 Answers: 2 Comments: 0

find ∫ x^2 (√((2−x)/(2+x)))dx

$$\mathrm{find}\:\int\:\mathrm{x}^{\mathrm{2}} \sqrt{\frac{\mathrm{2}−\mathrm{x}}{\mathrm{2}+\mathrm{x}}}\mathrm{dx} \\ $$

Question Number 98181 Answers: 0 Comments: 0

calculate ∫_0 ^π ln(x^2 −2xcosθ +1)dθ

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)\mathrm{d}\theta \\ $$

Question Number 98180 Answers: 0 Comments: 0

solve xy^(′′) +(x^3 +1)y =3e^(2x)

$$\mathrm{solve}\:\:\mathrm{xy}^{''} \:+\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)\mathrm{y}\:=\mathrm{3e}^{\mathrm{2x}} \\ $$

Question Number 98179 Answers: 2 Comments: 0

calculate ∫_1 ^(+∞) (dx/(x^2 (1−x^2 )^3 ))

$$\mathrm{calculate}\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$

Question Number 98178 Answers: 0 Comments: 0

calculate Σ_(p=0) ^n (z+1)^p with z root of x^2 −x+1=0

$$\mathrm{calculate}\:\:\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{p}} \\ $$$$\mathrm{with}\:\mathrm{z}\:\mathrm{root}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$

Question Number 98290 Answers: 0 Comments: 1

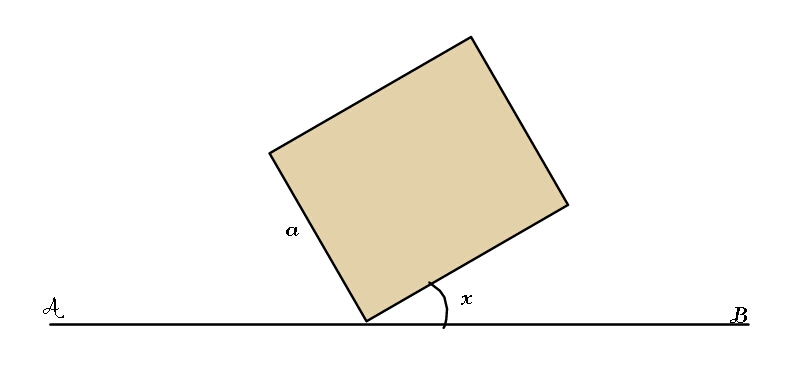
Question Number 98166 Answers: 0 Comments: 0

lim_(x→∞) [cos(2π((x/(x+1)))^a )]^x^2 a∈R

$$\underset{{x}\rightarrow\infty} {{lim}}\left[{cos}\left(\mathrm{2}\pi\left(\frac{{x}}{{x}+\mathrm{1}}\right)^{{a}} \right)\right]^{{x}^{\mathrm{2}} } \\ $$$${a}\in\mathbb{R} \\ $$

Question Number 98151 Answers: 2 Comments: 0

∫e^(x^5 +8x^2 ) dx =((√π)/(4(√2)))e^x^5 erfi(2(√2)x)−((5(√π))/(4(128)(√2)))(super−erf_((hyper)) (2(√2)x))+c where[super−erf_((hyper)) (t)] is super−function in D_2 and [D_n ]

$$\int{e}^{{x}^{\mathrm{5}} +\mathrm{8}{x}^{\mathrm{2}} } {dx} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{2}}}{e}^{{x}^{\mathrm{5}} } {erfi}\left(\mathrm{2}\sqrt{\mathrm{2}}{x}\right)−\frac{\mathrm{5}\sqrt{\pi}}{\mathrm{4}\left(\mathrm{128}\right)\sqrt{\mathrm{2}}}\left({super}−{erf}_{\left({hyper}\right)} \left(\mathrm{2}\sqrt{\mathrm{2}}{x}\right)\right)+{c} \\ $$$$ \\ $$$${where}\left[{super}−{erf}_{\left({hyper}\right)} \left({t}\right)\right]\:{is}\:{super}−{function} \\ $$$${in}\:{D}_{\mathrm{2}} \:{and}\:\left[{D}_{{n}} \right] \\ $$

Question Number 98149 Answers: 1 Comments: 1

Question Number 98148 Answers: 0 Comments: 0

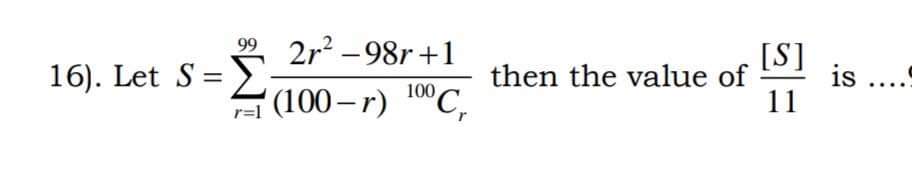
Question Number 98142 Answers: 0 Comments: 0

A man arrives at a bus stop in between 12:00pm and 12:15pm. Assuming a bus arrives the bus stop every 15 minutes, find the probability of him getting a bus in less than 5 minutes.

$$\mathcal{A}\:\mathrm{man}\:\mathrm{arrives}\:\mathrm{at}\:\mathrm{a}\:\mathrm{bus}\:\mathrm{stop}\:\mathrm{in}\:\mathrm{between}\:\mathrm{12}:\mathrm{00pm}\:\mathrm{and} \\ $$$$\mathrm{12}:\mathrm{15pm}.\:\mathrm{Assuming}\:\mathrm{a}\:\mathrm{bus}\:\mathrm{arrives}\:\mathrm{the}\:\mathrm{bus}\:\mathrm{stop}\:\mathrm{every} \\ $$$$\mathrm{15}\:\mathrm{minutes},\:\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\:\mathrm{him}\:\mathrm{getting}\:\mathrm{a}\:\mathrm{bus}\:\mathrm{in} \\ $$$$\mathrm{less}\:\mathrm{than}\:\mathrm{5}\:\mathrm{minutes}. \\ $$

Pg 1182 Pg 1183 Pg 1184 Pg 1185 Pg 1186 Pg 1187 Pg 1188 Pg 1189 Pg 1190 Pg 1191

Contact: info@tinkutara.com