Question and Answers Forum

AllQuestion and Answers: Page 1185

Question Number 98464 Answers: 1 Comments: 0

Working individually, A, B and C can finish a piece of work in 16 days, 20 days and 30 days respectively. In how many days can A, B and C together complete a work which is 3(1/2) times the previous work?

$$\mathrm{Working}\:\mathrm{individually},\:\mathrm{A},\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{can} \\ $$$$\mathrm{finish}\:\mathrm{a}\:\mathrm{piece}\:\mathrm{of}\:\mathrm{work}\:\mathrm{in}\:\mathrm{16}\:\mathrm{days},\:\mathrm{20}\:\mathrm{days} \\ $$$$\mathrm{and}\:\mathrm{30}\:\mathrm{days}\:\mathrm{respectively}.\:\mathrm{In}\:\mathrm{how}\:\mathrm{many} \\ $$$$\mathrm{days}\:\mathrm{can}\:\mathrm{A},\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{together}\:\mathrm{complete} \\ $$$$\mathrm{a}\:\mathrm{work}\:\mathrm{which}\:\mathrm{is}\:\mathrm{3}\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{times}\:\mathrm{the}\:\mathrm{previous} \\ $$$$\mathrm{work}? \\ $$

Question Number 98463 Answers: 1 Comments: 0

Question Number 98461 Answers: 3 Comments: 1

Question Number 98453 Answers: 0 Comments: 2

(m/(1×2))×(m/(2×3))×(m/(3×4))×...×(m/(99×100))=99 m?

$$\frac{{m}}{\mathrm{1}×\mathrm{2}}×\frac{{m}}{\mathrm{2}×\mathrm{3}}×\frac{{m}}{\mathrm{3}×\mathrm{4}}×...×\frac{{m}}{\mathrm{99}×\mathrm{100}}=\mathrm{99} \\ $$$$ \\ $$$${m}? \\ $$

Question Number 98613 Answers: 0 Comments: 0

Question Number 98450 Answers: 0 Comments: 1

Find the supremum and the infimum of f(x) = (x/(sin x)) ,x∈ (0,(π/2) ]

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{supremum}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{infimum}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}\:,\mathrm{x}\in\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\:\right] \\ $$

Question Number 98448 Answers: 1 Comments: 5

6^(273) +8^(273) :49 prove the division

$$\:\:\:\:\:\:\:\mathrm{6}^{\mathrm{273}} +\mathrm{8}^{\mathrm{273}} \:\::\mathrm{49}\:\:\:\boldsymbol{{prove}}\:\:\boldsymbol{{the}}\:\:\boldsymbol{{divi}\mathrm{s}{ion}} \\ $$

Question Number 98445 Answers: 2 Comments: 0

give at form of serie U_n =∫_0 ^1 ((x^n ln(x))/((1+x)^2 ))dx

$$\mathrm{give}\:\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 98444 Answers: 1 Comments: 0

calculate ∫_0 ^1 ((lnx)/((1+x)^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 98443 Answers: 1 Comments: 0

Given the sequence (U_n )_(n∈N) defined by U_0 =1 and U_(n+1) =f(U_n ) where f(x)=(x/((x+1)^2 )) Show by mathematical induction that ∀n∈N^∗ 0<U_n ≤(1/n)

$$\mathcal{G}\mathrm{iven}\:\mathrm{the}\:\mathrm{sequence}\:\left(\mathrm{U}_{\mathrm{n}} \right)_{\mathrm{n}\in\mathbb{N}} \:\mathrm{defined}\:\mathrm{by}\:\mathrm{U}_{\mathrm{0}} =\mathrm{1}\:\mathrm{and} \\ $$$$\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\mathrm{f}\left(\mathrm{U}_{\mathrm{n}} \right)\:\mathrm{where}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$\mathcal{S}\mathrm{how}\:\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{that}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$$$\mathrm{0}<\mathrm{U}_{\mathrm{n}} \leqslant\frac{\mathrm{1}}{\mathrm{n}} \\ $$

Question Number 98434 Answers: 0 Comments: 5

prove that Ω=Σ_(n=0) ^(+∞) Σ_(m=0 ) ^(+∞) ((Γ(n+(1/2)).Γ(m+(1/2)))/(Γ(n+1).Γ(m+1))).((((2/3))^n .((1/2))^m )/((n+m+(1/2)))) =((√3)/(2(√2))).G_(2,2) ^(2,2) ((1/4)∣_(0 , 0) ^((1/2),(1/2)) ) =(((√3)π)/(√2))K((3/4))=(((√3)π^2 )/(2(√2)AGM(1,(1/2))))

Question Number 98430 Answers: 1 Comments: 0

let g(x) =(2/(cos(πx))) developp g at fourier serie

$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{cos}\left(\pi\mathrm{x}\right)}\:\:\mathrm{developp}\:\mathrm{g}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 98429 Answers: 1 Comments: 0

let f(x) =cos(αx) developp f at fourier serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{cos}\left(\alpha\mathrm{x}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 98416 Answers: 3 Comments: 0

Question Number 98408 Answers: 1 Comments: 0

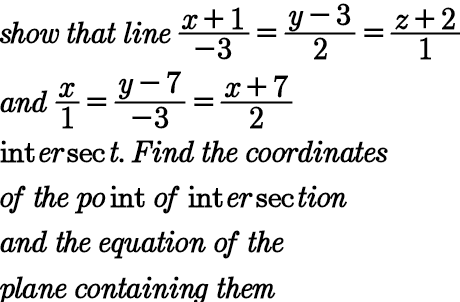
Question Number 98405 Answers: 1 Comments: 0

Question Number 98406 Answers: 0 Comments: 0

NB:P(E) means a set of all part of E

$$\boldsymbol{{NB}}:\boldsymbol{\mathcal{P}}\left(\boldsymbol{\mathrm{E}}\right)\:\mathrm{means}\:\mathrm{a}\:\mathrm{set}\:\mathrm{of}\:\mathrm{all}\:\mathrm{part}\:\mathrm{of}\:\boldsymbol{\mathrm{E}} \\ $$

Question Number 98398 Answers: 4 Comments: 2

f(x) = (√(x+(√(x+(√(x+(√(x+(√(x+...)))))))))) f ′(5) =

$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+...}}}}} \\ $$$$\mathrm{f}\:'\left(\mathrm{5}\right)\:=\: \\ $$

Question Number 98428 Answers: 1 Comments: 0

let f(x)=x^2 ,2π periodi even developp f at fourier serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \:\:,\mathrm{2}\pi\:\mathrm{periodi}\:\mathrm{even}\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 98426 Answers: 2 Comments: 0

let f(x) =∫_(π/4) ^(π/3) (dt/(x+tant)) calculate f(x) 2)explicit g(x) =∫_(π/4) ^(π/3) (dt/((x+tant)^2 )) 3) find the value of integrals ∫_(π/4) ^(π/3) (dt/(2+tant)) and ∫_(π/4) ^(π/3) (dt/((2+tant)^2 ))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{dt}}{\mathrm{x}+\mathrm{tant}}\:\:\mathrm{calculate}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{explicit}\:\mathrm{g}\left(\mathrm{x}\right)\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{dt}}{\left(\mathrm{x}+\mathrm{tant}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{integrals}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{dt}}{\mathrm{2}+\mathrm{tant}}\:\mathrm{and}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{dt}}{\left(\mathrm{2}+\mathrm{tant}\right)^{\mathrm{2}} } \\ $$

Question Number 98425 Answers: 0 Comments: 0

let f(x) =e^(−x) arctan(πx) 1) calculate f^((n)) (x)and f^((n)) (0) 2) developp f at integr serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{x}} \:\mathrm{arctan}\left(\pi\mathrm{x}\right) \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$

Question Number 98424 Answers: 1 Comments: 0

calculste A_n =∫_(−(1/2)) ^(1/2) x^n (√((1−x)/(1+x)))dx find nature of the serie Σ A_n

$$\mathrm{calculste}\:\mathrm{A}_{\mathrm{n}} =\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{n}} \sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}\mathrm{dx} \\ $$$$\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{the}\:\mathrm{serie}\:\Sigma\:\mathrm{A}_{\mathrm{n}} \\ $$

Question Number 98423 Answers: 1 Comments: 0

calculate ∫_0 ^∞ e^(−x^2 −(1/x^2 )) dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \mathrm{dx} \\ $$

Question Number 98382 Answers: 0 Comments: 2

∫ tan x (√(1+tan^4 x)) dx

$$\int\:\mathrm{tan}\:\mathrm{x}\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} \:\mathrm{x}}\:\mathrm{dx}\: \\ $$

Question Number 98380 Answers: 3 Comments: 0

let {u_n } and {v_n } be sequences defined by u_0 = 9, u_(n+1) = (1/2)u_n −3. v_n = u_n + 6. Calculate P_n = Σ_(i=0) ^n V_i in terms of n, the deduce Q_n = Σ_(i=0) ^n u_i using the above expressions find lim_(x→∞) Q_n .

$$\mathrm{let}\:\left\{{u}_{{n}} \right\}\:\mathrm{and}\:\left\{{v}_{{n}} \right\}\:\mathrm{be}\:\mathrm{sequences}\:\mathrm{defined}\:\mathrm{by} \\ $$$$\:{u}_{\mathrm{0}} \:=\:\mathrm{9},\:{u}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}} −\mathrm{3}. \\ $$$${v}_{{n}} \:=\:{u}_{{n}} \:+\:\mathrm{6}. \\ $$$$\mathrm{Calculate}\:{P}_{{n}} \:=\:\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{V}_{{i}} \:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{n},\:\mathrm{the}\:\mathrm{deduce}\:{Q}_{{n}} \:=\:\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{i}} \\ $$$$\mathrm{using}\:\mathrm{the}\:\mathrm{above}\:\mathrm{expressions}\:\mathrm{find} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{Q}_{{n}} \:. \\ $$

Question Number 98369 Answers: 2 Comments: 0

If A, B are two square matrices such that AB = A and BA = B, then

$$\mathrm{If}\:{A},\:{B}\:\mathrm{are}\:\mathrm{two}\:\mathrm{square}\:\mathrm{matrices}\:\mathrm{such} \\ $$$$\mathrm{that}\:{AB}\:=\:{A}\:\mathrm{and}\:{BA}\:=\:{B},\:\mathrm{then} \\ $$

Pg 1180 Pg 1181 Pg 1182 Pg 1183 Pg 1184 Pg 1185 Pg 1186 Pg 1187 Pg 1188 Pg 1189

Contact: info@tinkutara.com