Question and Answers Forum

AllQuestion and Answers: Page 1171

Question Number 99923 Answers: 0 Comments: 2

Eliminate arbitrary constant a and b from z = (x−a)^2 +(y−b)^2 to form the partial differential equation.

$$\mathrm{Eliminate}\:\mathrm{arbitrary}\:\mathrm{constant}\: \\ $$$${a}\:\mathrm{and}\:{b}\:\mathrm{from}\:\mathrm{z}\:=\:\left(\mathrm{x}−{a}\right)^{\mathrm{2}} +\left(\mathrm{y}−{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{to}\:\mathrm{form}\:\mathrm{the}\:\mathrm{partial}\:\mathrm{differential} \\ $$$$\mathrm{equation}.\: \\ $$

Question Number 99920 Answers: 3 Comments: 0

calculate Π_(n=2) ^∞ ((n^3 −1)/(n^3 +1))

$$\mathrm{calculate}\:\prod_{\mathrm{n}=\mathrm{2}} ^{\infty} \frac{\mathrm{n}^{\mathrm{3}} −\mathrm{1}}{\mathrm{n}^{\mathrm{3}} +\mathrm{1}} \\ $$

Question Number 99919 Answers: 1 Comments: 0

f_n is fibonacci sequence 1) find lim_(n→+∞) (f_(n+1) /(fn)) 2)prove that Σ f_n is convergente

$$\mathrm{f}_{\mathrm{n}} \mathrm{is}\:\mathrm{fibonacci}\:\mathrm{sequence} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{f}_{\mathrm{n}+\mathrm{1}} }{{fn}} \\ $$$$\left.\mathrm{2}\right){prove}\:{th}\mathrm{a}{t}\:\Sigma\:\mathrm{f}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{convergente} \\ $$

Question Number 99916 Answers: 1 Comments: 0

can anyone recommend a good textbook from which i can learn calculus..^

$$\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{anyone}}\:\boldsymbol{\mathrm{recommend}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{good}}\:\boldsymbol{\mathrm{textbook}} \\ $$$$\boldsymbol{\mathrm{from}}\:\boldsymbol{\mathrm{which}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{learn}}\:\boldsymbol{\mathrm{calculus}}.\hat {.} \\ $$

Question Number 99905 Answers: 0 Comments: 5

Question Number 99900 Answers: 0 Comments: 0

An insulated wire of diameter 1.22 mm carries a steady current of 5.4 A. The insulation material is 1.22 mm thick and has a? coeffiecient of thermal conductivity of 0.23 W/Km. the electrical resistivity of the material of the wire is 5.2 ×10^(−7) Ωm. find the temperature difference between the inner and outer surface of the insulated material when steady state is reached.

$$\mathrm{An}\:\mathrm{insulated}\:\mathrm{wire}\:\mathrm{of}\:\mathrm{diameter}\:\mathrm{1}.\mathrm{22}\:\mathrm{mm}\:\mathrm{carries}\:\mathrm{a}\:\mathrm{steady}\:\mathrm{current} \\ $$$$\mathrm{of}\:\mathrm{5}.\mathrm{4}\:\mathrm{A}.\:\mathrm{The}\:\mathrm{insulation}\:\mathrm{material}\:\mathrm{is}\:\mathrm{1}.\mathrm{22}\:\mathrm{mm}\:\mathrm{thick}\:\mathrm{and}\:\mathrm{has}\:\mathrm{a}? \\ $$$$\mathrm{coeffiecient}\:\mathrm{of}\:\mathrm{thermal}\:\mathrm{conductivity}\:\mathrm{of}\:\mathrm{0}.\mathrm{23}\:\mathrm{W}/\mathrm{Km}.\:\mathrm{the}\:\mathrm{electrical} \\ $$$$\mathrm{resistivity}\:\mathrm{of}\:\mathrm{the}\:\mathrm{material}\:\mathrm{of}\:\mathrm{the}\:\mathrm{wire}\:\mathrm{is}\:\mathrm{5}.\mathrm{2}\:×\mathrm{10}^{−\mathrm{7}} \Omega\mathrm{m}.\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{temperature}\:\mathrm{difference}\:\mathrm{between}\:\mathrm{the}\:\mathrm{inner}\:\mathrm{and}\:\mathrm{outer}\:\mathrm{surface}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{insulated}\:\mathrm{material}\:\mathrm{when}\:\mathrm{steady}\:\mathrm{state}\:\mathrm{is}\:\mathrm{reached}. \\ $$

Question Number 99895 Answers: 1 Comments: 0

Σ_(n=0) ^∞ (1/((3n+1)^3 ))=((13)/(27)) 𝛇(3) +((2𝛑^3 )/(81(√3)))

$$\:\:\:\:\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{3}\boldsymbol{{n}}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{13}}{\mathrm{27}}\:\boldsymbol{\zeta}\left(\mathrm{3}\right)\:+\frac{\mathrm{2}\boldsymbol{\pi}^{\mathrm{3}} }{\mathrm{81}\sqrt{\mathrm{3}}}\: \\ $$

Question Number 99894 Answers: 1 Comments: 0

Σ_(n≥0) (1/(n^2 +1)) = ?

$$\:\:\: \\ $$$$\underset{\boldsymbol{{n}}\geqslant\mathrm{0}} {\sum}\:\:\frac{\mathrm{1}}{\boldsymbol{{n}}^{\mathrm{2}} +\mathrm{1}}\:=\:? \\ $$

Question Number 99892 Answers: 0 Comments: 0

solve the equation xa^(1/x) +(1/x)a^x =2a Where a{−1,0,1}

$${solve}\:{the}\:{equation} \\ $$$${xa}^{\frac{\mathrm{1}}{{x}}} +\frac{\mathrm{1}}{{x}}{a}^{{x}} =\mathrm{2}{a} \\ $$$${Where}\:{a}\left\{−\mathrm{1},\mathrm{0},\mathrm{1}\right\} \\ $$

Question Number 99889 Answers: 1 Comments: 0

1+(1/2)+(1/3)+(1/4)+(1/5)+(1/6)+(1/7)+.......∞{Find the sum}

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}}+.......\infty\left\{\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\right\} \\ $$

Question Number 99887 Answers: 2 Comments: 5

Question Number 99877 Answers: 0 Comments: 5

Question Number 99869 Answers: 2 Comments: 0

tng(𝛑/9) + 4sin(𝛑/9) =(√3)

$$\:\boldsymbol{{tng}}\frac{\boldsymbol{\pi}}{\mathrm{9}}\:\:+\:\mathrm{4}\boldsymbol{{sin}}\frac{\boldsymbol{\pi}}{\mathrm{9}}\:=\sqrt{\mathrm{3}} \\ $$

Question Number 99853 Answers: 2 Comments: 0

(1/1^2 )+(1/2^2 )+(1/3^2 )+(1/4^2 )+(1/6^2 )+.....∞=?

$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{2}} }+.....\infty=? \\ $$

Question Number 99846 Answers: 0 Comments: 1

lim_(n→∞) (1−(1/(2!)))^(((1/(2!))−(1/(3!)))^(.........((1/(n!))−(1/((n+1)!)))) ) =?

$$\:\:\:\:\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}!}\right)^{\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)^{.........\left(\frac{\mathrm{1}}{\boldsymbol{{n}}!}−\frac{\mathrm{1}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)!}\right)} } =? \\ $$

Question Number 99839 Answers: 2 Comments: 4

let x_0 =1 and x_(n+1) =ln(e^x_n −x_n ) 1) prove that x_n →0 2)prove that Σ x_n converges and ddyermine its sum

$$\mathrm{let}\:\mathrm{x}_{\mathrm{0}} =\mathrm{1}\:\mathrm{and}\:\mathrm{x}_{\mathrm{n}+\mathrm{1}} =\mathrm{ln}\left(\mathrm{e}^{\mathrm{x}_{\mathrm{n}} } −\mathrm{x}_{\mathrm{n}} \right) \\ $$$$\left.\mathrm{1}\right)\:\mathrm{prove}\:\mathrm{that}\:\mathrm{x}_{\mathrm{n}} \:\rightarrow\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\mathrm{prove}\:\mathrm{that}\:\Sigma\:\mathrm{x}_{\mathrm{n}} \:\mathrm{converges}\:\mathrm{and}\:\mathrm{ddyermine}\:\mathrm{its}\:\mathrm{sum} \\ $$

Question Number 99832 Answers: 0 Comments: 0

solve x^2 y^(′′) −xy^′ +2y =x^3 e^(−x)

$$\mathrm{solve}\:\mathrm{x}^{\mathrm{2}} \mathrm{y}^{''} \:−\mathrm{xy}^{'} \:+\mathrm{2y}\:=\mathrm{x}^{\mathrm{3}} \mathrm{e}^{−\mathrm{x}} \\ $$

Question Number 99831 Answers: 0 Comments: 0

solve the ds { ((x^′ +2y^′ =sint)),((3x^′ +y^′ =te^t )) :}

$$\mathrm{solve}\:\mathrm{the}\:\mathrm{ds}\:\:\:\begin{cases}{\mathrm{x}^{'} \:+\mathrm{2y}^{'} \:=\mathrm{sint}}\\{\mathrm{3x}^{'} +\mathrm{y}^{'} \:=\mathrm{te}^{\mathrm{t}} }\end{cases} \\ $$

Question Number 99829 Answers: 0 Comments: 0

1.Find the principal if its interest in 3month with 5(1/2)% per amount is Rs.66. 2. The length of arectangular room is double of its breadth and height is one third of the length. If the room contains 972 cubic meter of air, find the area of floor of the room.

$$\:\mathrm{1}.\mathrm{Find}\:\mathrm{the}\:\mathrm{principal}\:\mathrm{if}\:\mathrm{its}\:\mathrm{interest}\:\mathrm{in}\:\mathrm{3month}\:\mathrm{with}\:\mathrm{5}\frac{\mathrm{1}}{\mathrm{2}}\%\:\mathrm{per}\:\mathrm{amount}\:\mathrm{is}\:\mathrm{Rs}.\mathrm{66}. \\ $$$$\:\mathrm{2}.\:\mathrm{The}\:\mathrm{length}\:\mathrm{of}\:\mathrm{arectangular}\:\mathrm{room}\:\mathrm{is}\:\mathrm{double}\:\mathrm{of}\:\mathrm{its}\:\mathrm{breadth}\:\mathrm{and} \\ $$$$\:\:\mathrm{height}\:\mathrm{is}\:\mathrm{one}\:\mathrm{third}\:\mathrm{of}\:\mathrm{the}\:\mathrm{length}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{room}\:\mathrm{contains}\:\mathrm{972}\:\mathrm{cubic}\:\mathrm{meter}\:\mathrm{of}\:\mathrm{air}, \\ $$$$\:\mathrm{find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{floor}\:\mathrm{of}\:\mathrm{the}\:\mathrm{room}. \\ $$

Question Number 99828 Answers: 1 Comments: 2

let A = (((2 1)),((1 2)) ) 1) calculate A^n 2)determine cosA and sinA 3) find chA and shA

$$\mathrm{let}\:\mathrm{A}\:=\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{A}^{\mathrm{n}} \\ $$$$\left.\mathrm{2}\right)\mathrm{determine}\:\mathrm{cosA}\:\mathrm{and}\:\mathrm{sinA} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{find}\:\mathrm{chA}\:\mathrm{and}\:\mathrm{shA} \\ $$

Question Number 99827 Answers: 0 Comments: 0

How many days after 12/7/1941 (pearl harbour bombed) was 9/11/2001 (the september 11 terrorist attack? please help, i′m having 27175days, which apparently isn′t correct.

$$\mathrm{How}\:\mathrm{many}\:\mathrm{days}\:\mathrm{after}\:\mathrm{12}/\mathrm{7}/\mathrm{1941} \\ $$$$\left(\mathrm{pearl}\:\mathrm{harbour}\:\mathrm{bombed}\right)\:\mathrm{was}\:\mathrm{9}/\mathrm{11}/\mathrm{2001} \\ $$$$\left(\mathrm{the}\:\mathrm{september}\:\mathrm{11}\:\mathrm{terrorist}\:\mathrm{attack}?\right. \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{help},\:\mathrm{i}'\mathrm{m}\:\mathrm{having}\:\mathrm{27175days},\: \\ $$$$\mathrm{which}\:\mathrm{apparently}\:\mathrm{isn}'\mathrm{t}\:\mathrm{correct}. \\ $$

Question Number 99824 Answers: 1 Comments: 0

calculate ∫_0 ^1 xe^(−x^2 ) arctan((2/x))dx

$$\mathrm{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{arctan}\left(\frac{\mathrm{2}}{\mathrm{x}}\right)\mathrm{dx} \\ $$

Question Number 99822 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((ch(sinx))/((x^2 +3)^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ch}\left(\mathrm{sinx}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 99820 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((x^2 dx)/((x^4 −x^2 +1)^2 ))

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$

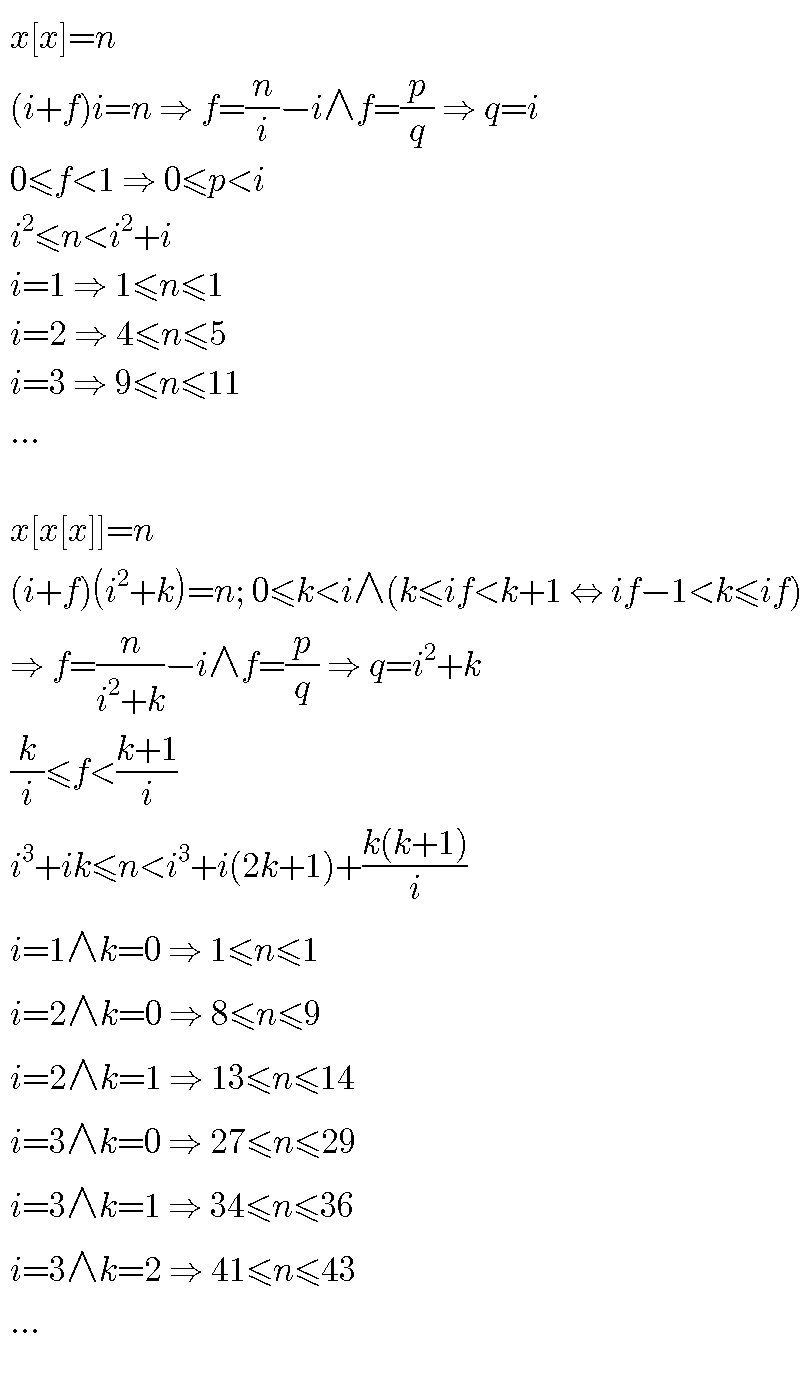
Question Number 99819 Answers: 0 Comments: 0

sove sinx y^′ −cos(2x)y =xe^(−x)

$$\mathrm{sove}\:\:\mathrm{sinx}\:\mathrm{y}^{'} \:−\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{y}\:=\mathrm{xe}^{−\mathrm{x}} \\ $$

Question Number 99818 Answers: 2 Comments: 0

∫_0 ^1 ln(1+(1/(n^2 x^2 )))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$

Pg 1166 Pg 1167 Pg 1168 Pg 1169 Pg 1170 Pg 1171 Pg 1172 Pg 1173 Pg 1174 Pg 1175

Contact: info@tinkutara.com