Question and Answers Forum

AllQuestion and Answers: Page 1167

Question Number 97007 Answers: 0 Comments: 16

Question Number 97005 Answers: 1 Comments: 2

Question Number 97001 Answers: 1 Comments: 2

solve (1+x^2 ) (dy/dx) = xy−xy^2

$$\mathrm{solve}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{xy}−\mathrm{xy}^{\mathrm{2}} \\ $$

Question Number 96990 Answers: 1 Comments: 0

∫_0 ^1 ((√x))^(√x) dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)^{\sqrt{\mathrm{x}}} \mathrm{dx} \\ $$

Question Number 96979 Answers: 1 Comments: 0

∫_0 ^π arctan(3^(cos(x)) )dx

$$\int_{\mathrm{0}} ^{\pi} {arctan}\left(\mathrm{3}^{{cos}\left({x}\right)} \right){dx} \\ $$

Question Number 96977 Answers: 1 Comments: 0

lim_(x→5) ((x − 5)/(2 + cot^2 (2/(x −5))))

$$\underset{{x}\rightarrow\mathrm{5}} {\mathrm{lim}}\:\frac{{x}\:−\:\mathrm{5}}{\mathrm{2}\:+\:\mathrm{cot}^{\mathrm{2}} \frac{\mathrm{2}}{{x}\:−\mathrm{5}}} \\ $$

Question Number 96962 Answers: 1 Comments: 0

find ∫_0 ^1 (dx/((√(x+1))+(√(2x^2 +1))))

$$\mathrm{find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\sqrt{\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}}} \\ $$

Question Number 96959 Answers: 1 Comments: 0

find ∫ arctan(x−(1/x))dx

$$\mathrm{find}\:\int\:\mathrm{arctan}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx} \\ $$

Question Number 96958 Answers: 0 Comments: 0

let g(x) =ln(tanx) developp f at fourier serie

$$\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{tanx}\right) \\ $$$$\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 96957 Answers: 2 Comments: 0

find ∫ x^3 (√(2−x−x^2 ))dx

$$\mathrm{find}\:\int\:\mathrm{x}^{\mathrm{3}} \sqrt{\mathrm{2}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 96956 Answers: 2 Comments: 0

calculate ∫_(−∞) ^∞ ((x^2 −3)/((x^2 −x+1)^3 ))dx

$$\mathrm{calculate}\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$

Question Number 96955 Answers: 1 Comments: 0

let f(x) =ln(1+sinx) developp f at fourier serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{1}+\mathrm{sinx}\right)\: \\ $$$$\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 96951 Answers: 1 Comments: 5

prove that 1−(1/2)+(1/3)−(1/4)+(1/5)+...+((−1^(n−1) )/n) is always positive

$${prove}\:{that}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+...+\frac{−\mathrm{1}^{{n}−\mathrm{1}} }{{n}}\:\:{is}\:{always}\:{positive} \\ $$$$ \\ $$

Question Number 96947 Answers: 0 Comments: 4

Question Number 96936 Answers: 2 Comments: 1

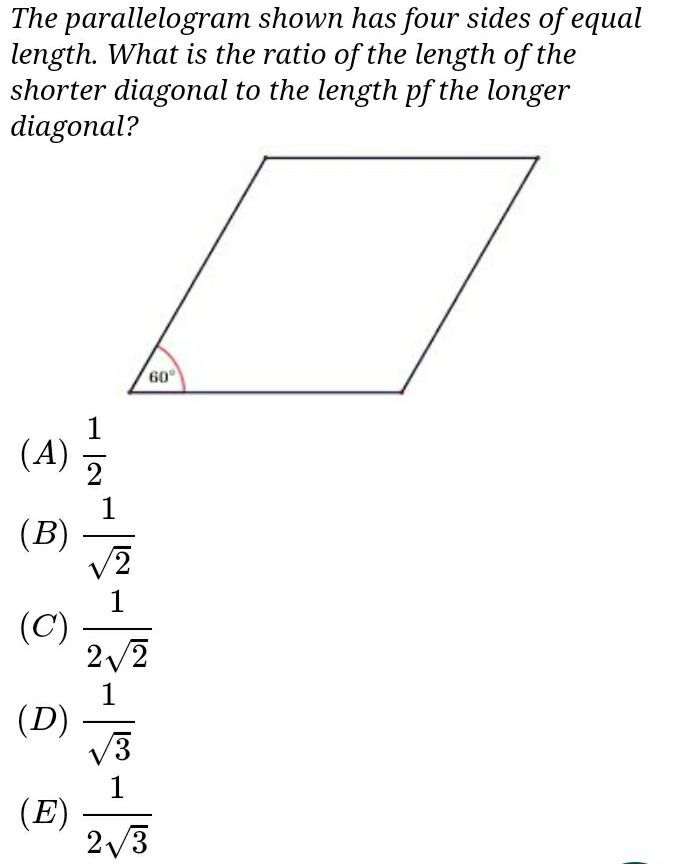
Question Number 96931 Answers: 2 Comments: 3

lim_(x→∞) ((5x^4 −8)/(7x^3 +2))×tan ((3/x)) =?

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{5x}^{\mathrm{4}} −\mathrm{8}}{\mathrm{7x}^{\mathrm{3}} +\mathrm{2}}×\mathrm{tan}\:\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\:=? \\ $$

Question Number 96930 Answers: 0 Comments: 1

E(x) denotes the integer part of x x∈]0;1[ determine: E(x^x ) and E(x^x^x ) calcul lim_(x→0) E(x^x^x ) please i need help please

$${E}\left({x}\right)\:{denotes}\:{the}\:{integer}\:{part}\:{of}\:{x}\: \\ $$$$\left.{x}\in\right]\mathrm{0};\mathrm{1}\left[\:{determine}:\right. \\ $$$$\boldsymbol{{E}}\left(\boldsymbol{{x}}^{\boldsymbol{{x}}} \right)\:\boldsymbol{{and}}\:\boldsymbol{{E}}\left(\boldsymbol{{x}}^{\boldsymbol{{x}}^{\boldsymbol{{x}}} } \right)\: \\ $$$$\boldsymbol{{calcul}}\:\boldsymbol{{li}}\underset{{x}\rightarrow\mathrm{0}} {\boldsymbol{{m}}}\:\boldsymbol{{E}}\left(\boldsymbol{{x}}^{\boldsymbol{{x}}^{\boldsymbol{{x}}} } \right) \\ $$$$\boldsymbol{{please}}\:\boldsymbol{{i}}\:\boldsymbol{{need}}\:\boldsymbol{{help}}\:\boldsymbol{{please}} \\ $$

Question Number 96928 Answers: 3 Comments: 1

69x ≡ 1 (mod 31) solve for x

$$\mathrm{69}{x}\:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{31}\right)\: \\ $$$$\mathrm{solve}\:\mathrm{for}\:{x} \\ $$

Question Number 96925 Answers: 2 Comments: 0

∫_0 ^1 ((ln(x^2 +1))/(x+1))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}+\mathrm{1}}{dx} \\ $$

Question Number 96922 Answers: 0 Comments: 8

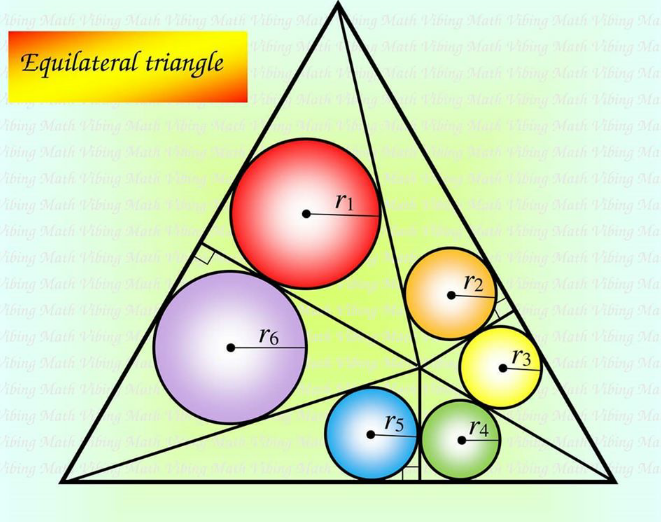
Question Number 96920 Answers: 0 Comments: 2

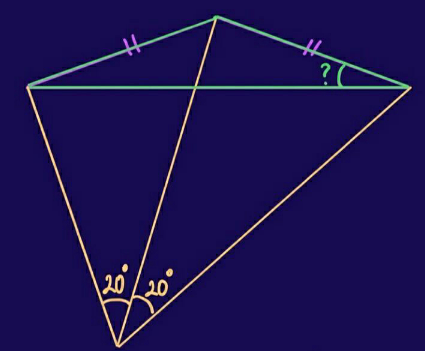
Question Number 96911 Answers: 1 Comments: 2

∫_(−∞) ^(+∞) ((x^2 sinh(x)+tan^(−1) (x)∙log(x^4 +1))/(πe^x^2 +((x^8 +3cosh(x)))^(1/3) ))dx

$$\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{sinh}\left(\mathrm{x}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\centerdot\mathrm{log}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)}{\pi\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\sqrt[{\mathrm{3}}]{\mathrm{x}^{\mathrm{8}} +\mathrm{3cosh}\left(\mathrm{x}\right)}}\mathrm{dx} \\ $$

Question Number 96907 Answers: 0 Comments: 1

Σ_(z = 0) ^(10) cos^3 (((πz)/3)) = ?

$$\underset{\mathrm{z}\:=\:\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\:\mathrm{cos}\:^{\mathrm{3}} \left(\frac{\pi\mathrm{z}}{\mathrm{3}}\right)\:=\:? \\ $$

Question Number 96906 Answers: 1 Comments: 0

Question Number 96904 Answers: 0 Comments: 3

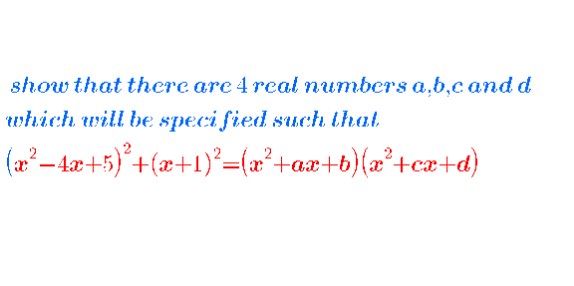
Question Number 96898 Answers: 2 Comments: 1

Pg 1162 Pg 1163 Pg 1164 Pg 1165 Pg 1166 Pg 1167 Pg 1168 Pg 1169 Pg 1170 Pg 1171

Contact: info@tinkutara.com