
AllQuestion and Answers: Page 1161
Question Number 101940 Answers: 1 Comments: 0
Question Number 101937 Answers: 0 Comments: 0
Question Number 101921 Answers: 1 Comments: 1
Question Number 101891 Answers: 3 Comments: 0
Question Number 101888 Answers: 3 Comments: 1
Question Number 102323 Answers: 2 Comments: 0
Question Number 102313 Answers: 2 Comments: 0

Question Number 101882 Answers: 1 Comments: 1
Question Number 101880 Answers: 2 Comments: 0
Question Number 105257 Answers: 2 Comments: 0
$${y}''−\mathrm{2}{y}'+{y}\:=\:{xe}^{{x}} \mathrm{sin}\:{x}\: \\ $$
Question Number 105256 Answers: 0 Comments: 0
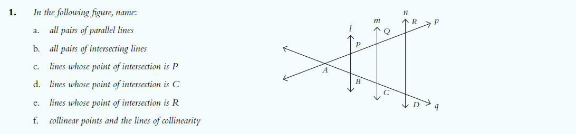
Question Number 101848 Answers: 2 Comments: 0
Question Number 101846 Answers: 2 Comments: 0
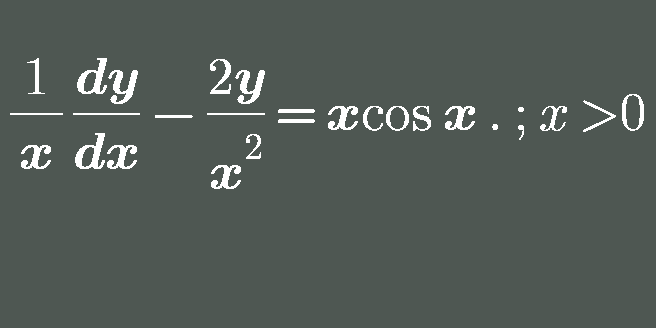
Question Number 101841 Answers: 1 Comments: 0
Question Number 101835 Answers: 3 Comments: 0
Question Number 101833 Answers: 3 Comments: 0
$$\int\:_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\:{dx}\:?\: \\ $$
Question Number 101832 Answers: 0 Comments: 1
Question Number 101828 Answers: 2 Comments: 0
Question Number 101822 Answers: 1 Comments: 0
Question Number 101816 Answers: 1 Comments: 0
Question Number 101808 Answers: 2 Comments: 0
Question Number 101803 Answers: 1 Comments: 2
Question Number 101800 Answers: 1 Comments: 3

Question Number 101794 Answers: 1 Comments: 0
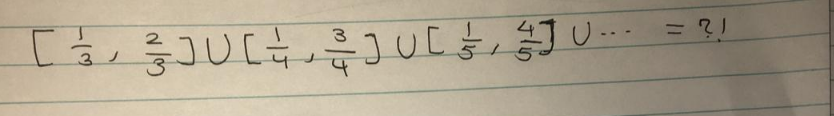
Question Number 101793 Answers: 1 Comments: 0
Question Number 101791 Answers: 2 Comments: 0
Pg 1156 Pg 1157 Pg 1158 Pg 1159 Pg 1160 Pg 1161 Pg 1162 Pg 1163 Pg 1164 Pg 1165
