Question and Answers Forum

AllQuestion and Answers: Page 1153

Question Number 101366 Answers: 1 Comments: 2

lim_(x→0) ((x^3 −sin^3 x)/x^5 ) =?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{sin}\:^{\mathrm{3}} {x}}{{x}^{\mathrm{5}} }\:=? \\ $$

Question Number 101363 Answers: 1 Comments: 0

The solution set of inequality (((√((3x−7)^2 ))−2)/(x−3)) ≤ ((3−(√x^2 ))/(x−3)) is __ (A) (−∞, (1/2)] (D) [(1/2), ∞) (B) [(1/2),1 ] (E) (−∞,(2/3)] (C) (−∞,1 ]

$$\mathrm{The}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\mathrm{inequality} \\ $$$$\frac{\sqrt{\left(\mathrm{3x}−\mathrm{7}\right)^{\mathrm{2}} }−\mathrm{2}}{\mathrm{x}−\mathrm{3}}\:\leqslant\:\frac{\mathrm{3}−\sqrt{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}−\mathrm{3}}\:\mathrm{is}\:\_\_ \\ $$$$\left(\mathrm{A}\right)\:\left(−\infty,\:\frac{\mathrm{1}}{\mathrm{2}}\right]\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\left[\frac{\mathrm{1}}{\mathrm{2}},\:\infty\right) \\ $$$$\left(\mathrm{B}\right)\:\left[\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\:\right]\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{E}\right)\:\left(−\infty,\frac{\mathrm{2}}{\mathrm{3}}\right] \\ $$$$\left(\mathrm{C}\right)\:\left(−\infty,\mathrm{1}\:\right]\: \\ $$

Question Number 101362 Answers: 0 Comments: 1

Question Number 101360 Answers: 0 Comments: 0

xy′=y(ylnx+1)

$${xy}'={y}\left({ylnx}+\mathrm{1}\right) \\ $$

Question Number 101350 Answers: 1 Comments: 0

Question Number 101345 Answers: 0 Comments: 3

(1)∫ ((sec^4 x tan x)/(sec^4 x+4)) dx= (2) ∫x^(2x) (2lnx +2) dx = (3) ∫_0 ^1 (√(1−x^2 )) dx =

$$\left(\mathrm{1}\right)\int\:\frac{\mathrm{sec}\:^{\mathrm{4}} {x}\:\mathrm{tan}\:{x}}{\mathrm{sec}\:^{\mathrm{4}} {x}+\mathrm{4}}\:{dx}= \\ $$$$\left(\mathrm{2}\right)\:\int{x}^{\mathrm{2}{x}} \left(\mathrm{2ln}{x}\:+\mathrm{2}\right)\:{dx}\:= \\ $$$$\left(\mathrm{3}\right)\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:=\: \\ $$

Question Number 101342 Answers: 1 Comments: 0

find U_n =∫_0 ^1 ((x^(2n) −1)/(lnx))dx with n integr natural and n≥2 find nature of the serie Σ U_n

$$\mathrm{find}\:\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}} −\mathrm{1}}{\mathrm{lnx}}\mathrm{dx}\:\:\mathrm{with}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{natural}\:\mathrm{and}\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{the}\:\mathrm{serie}\:\Sigma\:\mathrm{U}_{\mathrm{n}} \\ $$

Question Number 101402 Answers: 0 Comments: 3

I desire the developmenter of this apps improve adding some other functions like as:choose whole text by tap in text or choose some line at one time has many colours more

$$\mathrm{I}\:\mathrm{desire}\:\mathrm{the}\:\mathrm{developmenter}\:\mathrm{of}\:\mathrm{this}\:\mathrm{apps} \\ $$$$\mathrm{improve}\:\mathrm{adding}\:\mathrm{some}\:\mathrm{other}\:\mathrm{functions} \\ $$$$\mathrm{like}\:\mathrm{as}:\mathrm{choose}\:\mathrm{whole}\:\mathrm{text}\:\mathrm{by}\:\mathrm{tap}\:\mathrm{in} \\ $$$$\mathrm{text}\:\mathrm{or}\:\mathrm{choose}\:\mathrm{some}\:\mathrm{line}\:\mathrm{at}\:\mathrm{one}\:\mathrm{time} \\ $$$$\mathrm{has}\:\mathrm{many}\:\mathrm{colours}\:\mathrm{more} \\ $$

Question Number 101330 Answers: 0 Comments: 5

Evaluate. ∫_(−π) ^π x^9 cos x dx

$${Evaluate}. \\ $$$$\int_{−\pi} ^{\pi} {x}^{\mathrm{9}} \mathrm{cos}\:{x}\:{dx} \\ $$

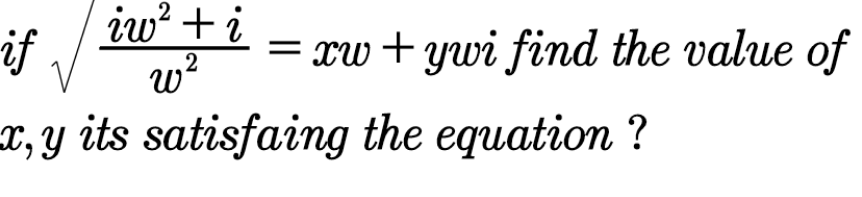
Question Number 101329 Answers: 1 Comments: 0

Question Number 101328 Answers: 0 Comments: 1

this i a beautifull old question in the forum by sir.Ali Esam i Reposted it trying to find any idea to solve I=∫_(−1) ^1 (((sin(x))/(sinh^(−1) (x))))(((sin^(−1) (x))/(sinh(x))))dx i solved it numerical the value is 2.03383

$${this}\:{i}\:{a}\:{beautifull}\:{old}\:{question}\:{in}\:{the}\:{forum} \\ $$$${by}\:{sir}.{Ali}\:{Esam}\:{i}\:{Reposted}\:{it}\:{trying}\:{to} \\ $$$${find}\:{any}\:{idea}\:{to}\:{solve} \\ $$$$ \\ $$$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\frac{{sin}\left({x}\right)}{{sinh}^{−\mathrm{1}} \left({x}\right)}\right)\left(\frac{{sin}^{−\mathrm{1}} \left({x}\right)}{{sinh}\left({x}\right)}\right){dx} \\ $$$$ \\ $$$${i}\:{solved}\:{it}\:{numerical}\: \\ $$$${the}\:{value}\:{is}\:\mathrm{2}.\mathrm{03383} \\ $$

Question Number 101319 Answers: 1 Comments: 4

find the area bounded the parabola y=4x^2 and y=8−4x^2 ? by using intigral? help me

$${find}\:{the}\:{area}\:{bounded}\:{the}\:{parabola}\: \\ $$$${y}=\mathrm{4}{x}^{\mathrm{2}} \:\:\:{and}\:\:{y}=\mathrm{8}−\mathrm{4}{x}^{\mathrm{2}} \:\:?\:\:{by}\:{using}\:{intigral}? \\ $$$${help}\:{me} \\ $$

Question Number 101273 Answers: 0 Comments: 0

caoculate lim_(x→0) ((sh(sin(2x))−sin(sh(2x)))/x^3 )

$$\mathrm{caoculate}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{sh}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)−\mathrm{sin}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$

Question Number 101272 Answers: 1 Comments: 2

∫(√(sec x)) dx

$$\int\sqrt{\mathrm{sec}\:{x}}\:{dx}\: \\ $$

Question Number 101271 Answers: 0 Comments: 2

find ∫ ((xdx)/((√(x^2 +x+1))+(√(x^2 −x+1))))

$$\mathrm{find}\:\int\:\:\:\frac{\mathrm{xdx}}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}} \\ $$

Question Number 101270 Answers: 0 Comments: 0

calculate ∫_1 ^(+∞) (dx/(x^2 (x+1)^2 (x+2)^2 (x+3)^2 ))

$$\mathrm{calculate}\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$

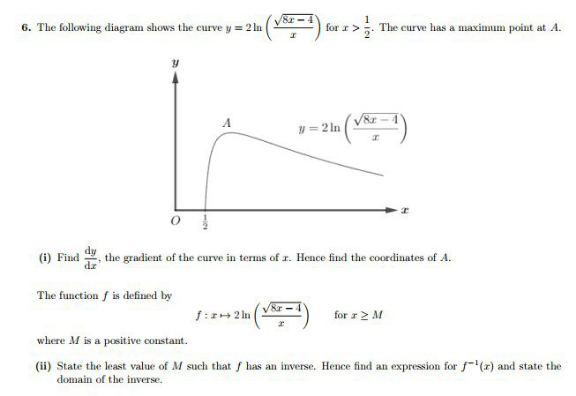
Question Number 101269 Answers: 1 Comments: 0

calculate ∫_4 ^(+∞) (dx/((x−2)^5 (x+3)^7 ))

$$\mathrm{calculate}\:\int_{\mathrm{4}} ^{+\infty} \:\:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{5}} \left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{7}} } \\ $$

Question Number 101268 Answers: 1 Comments: 0

calculate ∫_(−∞) ^∞ ((cos(arctan(2x+1)))/(x^2 +2x+2))dx

$$\mathrm{calculate}\:\int_{−\infty} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctan}\left(\mathrm{2x}+\mathrm{1}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}}\mathrm{dx} \\ $$

Question Number 101266 Answers: 0 Comments: 0

calculate ∫_1 ^(+∞) (dx/(x^2 (x+1)^3 (x+2)^4 ))

$$\mathrm{calculate}\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} } \\ $$

Question Number 101286 Answers: 0 Comments: 3

∫(((x^m −x^n )^2 )/(√x))dx=?

$$\int\frac{\left(\mathrm{x}^{\mathrm{m}} −\mathrm{x}^{\mathrm{n}} \right)^{\mathrm{2}} }{\sqrt{\mathrm{x}}}\mathrm{dx}=? \\ $$

Question Number 101258 Answers: 2 Comments: 2

minimum value f(x,y)=x^2 +y^2 with constrain g(x,y)= x^2 y−16

$$\mathrm{minimum}\:\mathrm{value}\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{with}\:\mathrm{constrain}\:\mathrm{g}\left(\mathrm{x},\mathrm{y}\right)=\:\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{16} \\ $$

Question Number 101252 Answers: 0 Comments: 1

(√(1+2(√(1+4(√(1+5(√(1+6(√(1+7(√(1+8..))))))))))))∞=?

$$\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{\mathrm{1}+\mathrm{6}\sqrt{\mathrm{1}+\mathrm{7}\sqrt{\mathrm{1}+\mathrm{8}..}}}}}}\infty=? \\ $$

Question Number 101250 Answers: 0 Comments: 0

Question Number 101249 Answers: 0 Comments: 8

As request by many users earlier, ability to convert written equations to plain text is now available. Plain text may be useful when you need to enter question content on internet sites. Standard convention for limits and power are used during processing and sites so one liner integral, summation, limits derviates should be directly usable. You might need do some small editing depending upon app used. Parser is implemented on server.

$$\mathrm{As}\:\mathrm{request}\:\mathrm{by}\:\mathrm{many}\:\mathrm{users}\:\mathrm{earlier}, \\ $$$$\mathrm{ability}\:\mathrm{to}\:\mathrm{convert}\:\mathrm{written}\:\mathrm{equations} \\ $$$$\mathrm{to}\:\mathrm{plain}\:\mathrm{text}\:\mathrm{is}\:\mathrm{now}\:\mathrm{available}. \\ $$$$\mathrm{Plain}\:\mathrm{text}\:\mathrm{may}\:\mathrm{be}\:\mathrm{useful}\:\mathrm{when}\:\mathrm{you} \\ $$$$\mathrm{need}\:\mathrm{to}\:\mathrm{enter}\:\mathrm{question}\:\mathrm{content} \\ $$$$\mathrm{on}\:\mathrm{internet}\:\mathrm{sites}. \\ $$$$\mathrm{Standard}\:\mathrm{convention}\:\mathrm{for}\:\mathrm{limits} \\ $$$$\mathrm{and}\:\mathrm{power}\:\mathrm{are}\:\mathrm{used}\:\mathrm{during}\:\mathrm{processing} \\ $$$$\mathrm{and}\:\mathrm{sites}\:\mathrm{so}\:\mathrm{one}\:\mathrm{liner}\:\mathrm{integral}, \\ $$$$\mathrm{summation},\:\mathrm{limits}\:\mathrm{derviates}\:\mathrm{should} \\ $$$$\mathrm{be}\:\mathrm{directly}\:\mathrm{usable}.\:\mathrm{You}\:\mathrm{might} \\ $$$$\mathrm{need}\:\mathrm{do}\:\mathrm{some}\:\mathrm{small}\:\mathrm{editing} \\ $$$$\mathrm{depending}\:\mathrm{upon}\:\mathrm{app}\:\mathrm{used}. \\ $$$$\boldsymbol{\mathrm{Parser}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{implemented}}\:\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{server}}. \\ $$

Question Number 101248 Answers: 0 Comments: 0

Π_(p∈P/(2..3)) ((1/p))^2 =? p is prime number Any help ?

$$\:\:\:\underset{\boldsymbol{{p}}\in\boldsymbol{{P}}/\left(\mathrm{2}..\mathrm{3}\right)} {\prod}\left(\frac{\mathrm{1}}{\boldsymbol{{p}}}\right)^{\mathrm{2}} =?\:\:\:\:\:\boldsymbol{{p}}\:{is}\:{prime}\:{number} \\ $$$${Any}\:{help}\:? \\ $$

Question Number 101247 Answers: 1 Comments: 0

Pg 1148 Pg 1149 Pg 1150 Pg 1151 Pg 1152 Pg 1153 Pg 1154 Pg 1155 Pg 1156 Pg 1157

Contact: info@tinkutara.com