
AllQuestion and Answers: Page 1147
Question Number 103196 Answers: 1 Comments: 0
Question Number 103195 Answers: 0 Comments: 1
$$\mathrm{893}{x}\:=\:\mathrm{266}\:\left({mod}\:\mathrm{2432}\right) \\ $$
Question Number 103193 Answers: 0 Comments: 1
$$\frac{{dy}}{{dx}}\:+\:{y}.\mathrm{cot}\:\left({x}\right)\:=\:\mathrm{sin}\:\left({x}\right) \\ $$
Question Number 103190 Answers: 1 Comments: 0
Question Number 103186 Answers: 0 Comments: 0
Question Number 103180 Answers: 0 Comments: 0
Question Number 103179 Answers: 1 Comments: 1
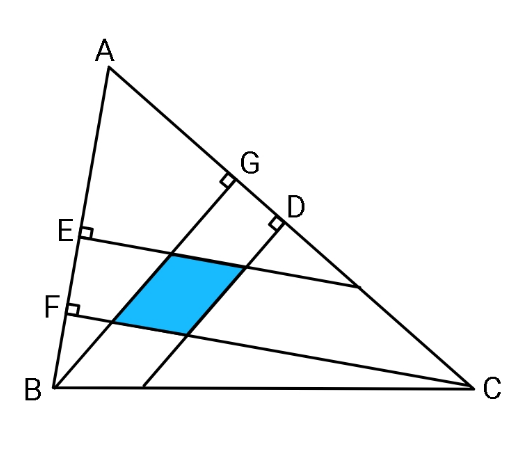
Question Number 103177 Answers: 1 Comments: 0
Question Number 103171 Answers: 1 Comments: 1

Question Number 103170 Answers: 0 Comments: 3
$${x}^{{x}^{{x}} } =\mathrm{3}\:\:\:\:\:\:{x}=? \\ $$$$ \\ $$
Question Number 103168 Answers: 1 Comments: 0
Question Number 103165 Answers: 0 Comments: 3
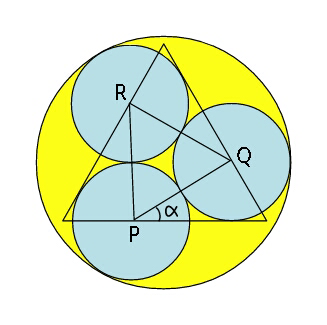
Question Number 103159 Answers: 0 Comments: 1
Question Number 103155 Answers: 0 Comments: 2
Question Number 103154 Answers: 2 Comments: 0
$$\int_{\mathrm{0}} ^{\mathrm{1}} {logxlog}\left(\mathrm{1}−{x}\right){dx} \\ $$
Question Number 103151 Answers: 0 Comments: 1
Question Number 103149 Answers: 2 Comments: 0
Question Number 103147 Answers: 2 Comments: 0

Question Number 103138 Answers: 1 Comments: 2
$$\left({D}^{\mathrm{2}} −\mathrm{4}{D}\right){y}\:=\:{x}^{\mathrm{2}} \:{e}^{\mathrm{2}{x}} \\ $$
Question Number 103130 Answers: 3 Comments: 1
Question Number 103124 Answers: 1 Comments: 0
Question Number 103120 Answers: 0 Comments: 0
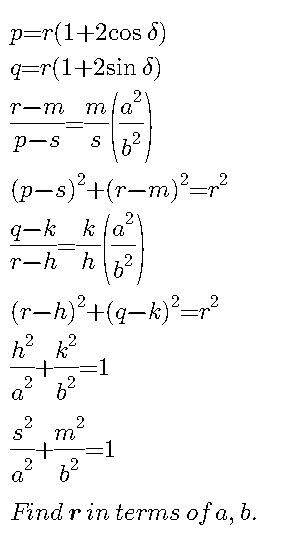
Question Number 103119 Answers: 0 Comments: 0
Question Number 103114 Answers: 1 Comments: 2

Question Number 103143 Answers: 1 Comments: 1

Question Number 103094 Answers: 0 Comments: 4
Pg 1142 Pg 1143 Pg 1144 Pg 1145 Pg 1146 Pg 1147 Pg 1148 Pg 1149 Pg 1150 Pg 1151
