Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1144

Question Number 103894 Answers: 3 Comments: 0

(d/(d((d/dx)sinx)))∙sinx=?

$$\frac{{d}}{{d}\left(\frac{{d}}{{dx}}{sinx}\right)}\centerdot{sinx}=? \\ $$

Question Number 103893 Answers: 0 Comments: 0

Question Number 103888 Answers: 2 Comments: 0

find all such numbers: if we make its last digit, say k, as its first digit, the number becomes k times large as before. (□□...□k)→(k□□...□)=k×(□□...□k)

$${find}\:{all}\:{such}\:{numbers}: \\ $$$${if}\:{we}\:{make}\:{its}\:{last}\:{digit},\:{say}\:{k},\:{as}\:{its} \\ $$$${first}\:{digit},\:{the}\:{number}\:{becomes}\:{k} \\ $$$${times}\:{large}\:{as}\:{before}. \\ $$$$\left(\Box\Box...\Box{k}\right)\rightarrow\left({k}\Box\Box...\Box\right)={k}×\left(\Box\Box...\Box{k}\right) \\ $$

Question Number 103881 Answers: 2 Comments: 0

Π_(n=1) ^∞ (((2n−1)(2n+1))/(4n^2 )) ?

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{4}{n}^{\mathrm{2}} }\:? \\ $$

Question Number 103879 Answers: 2 Comments: 2

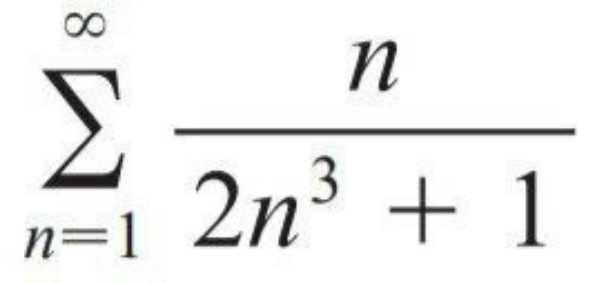
Question Number 103874 Answers: 1 Comments: 1

Question Number 103872 Answers: 0 Comments: 3

Question Number 103871 Answers: 1 Comments: 2

∫_0 ^1 ((x^(98) −99x+98)/(logx))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{98}} −\mathrm{99}{x}+\mathrm{98}}{{logx}}{dx} \\ $$

Question Number 103870 Answers: 0 Comments: 0

De^ montrer que la fonction f(x)=x^2 ∙sin((1/x)) admet un DL d′ordre 2.

$$\mathcal{D}\acute {\mathrm{e}montrer}\:\mathrm{que}\:\mathrm{la}\:\mathrm{fonction}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \centerdot\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{admet}\:\mathrm{un}\:\mathrm{DL}\:\mathrm{d}'\mathrm{ordre}\:\mathrm{2}. \\ $$

Question Number 103869 Answers: 0 Comments: 0

by using the Frobinus method solve the deffrentional equation xy^(′′) −2pxy^′ +(p(p+1)+b^2 x^2 )y=0 and give for example for this when p=1,b=2 such that (p,b) be areal number ?

$${by}\:{using}\:{the}\:{Frobinus}\:{method}\:{solve}\:{the}\:{deffrentional}\:{equation} \\ $$$${xy}^{''} −\mathrm{2}{pxy}^{'} +\left({p}\left({p}+\mathrm{1}\right)+{b}^{\mathrm{2}} {x}^{\mathrm{2}} \right){y}=\mathrm{0} \\ $$$$ \\ $$$${and}\:{give}\:{for}\:{example}\:{for}\:{this}\:{when}\:{p}=\mathrm{1},{b}=\mathrm{2}\: \\ $$$${such}\:{that}\:\left({p},{b}\right)\:{be}\:{areal}\:{number}\:? \\ $$

Question Number 103863 Answers: 8 Comments: 0

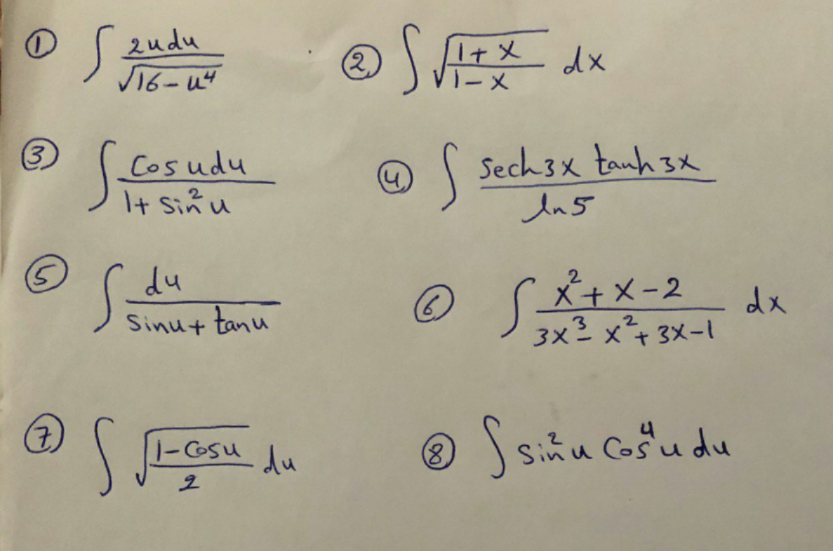
Question Number 103862 Answers: 0 Comments: 0

Question Number 103860 Answers: 2 Comments: 0

find ∫ (dx/(cos^4 x))

$$\mathrm{find}\:\int\:\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{4}} \mathrm{x}} \\ $$

Question Number 103846 Answers: 0 Comments: 2

∫(dx/(x^(1/3) +2))

$$\int\frac{{dx}}{{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}} \\ $$

Question Number 103995 Answers: 1 Comments: 0

solve y^(′′) +2y^′ −y =(e^(−x) /x)

$$\mathrm{solve}\:\mathrm{y}^{''} +\mathrm{2y}^{'} −\mathrm{y}\:=\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}} \\ $$

Question Number 103835 Answers: 0 Comments: 0

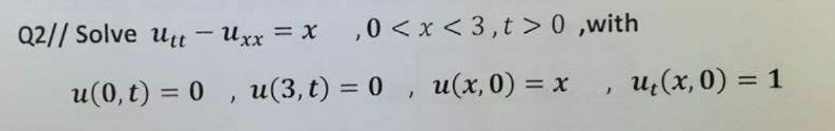
Question Number 103832 Answers: 1 Comments: 0

p(x) = x^4 +ax^3 +bx^2 +cx +d if p(1)=10,p(2)=20 and p(3)=30 . find ((p(12)+p(−8))/(10))

$${p}\left({x}\right)\:=\:{x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}\:+{d} \\ $$$${if}\:{p}\left(\mathrm{1}\right)=\mathrm{10},{p}\left(\mathrm{2}\right)=\mathrm{20}\:{and} \\ $$$${p}\left(\mathrm{3}\right)=\mathrm{30}\:.\:{find}\:\frac{{p}\left(\mathrm{12}\right)+{p}\left(−\mathrm{8}\right)}{\mathrm{10}} \\ $$

Question Number 103828 Answers: 1 Comments: 0

min{ ∫_0 ^1 (x^3 −px−q)^2 dx , (p,q)∈R^2 }

$$\:\:\:\:\:{min}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{3}} −{px}−{q}\right)^{\mathrm{2}} {dx}\:,\:\:\left({p},{q}\right)\in\mathbb{R}^{\mathrm{2}} \:\right\} \\ $$

Question Number 103825 Answers: 7 Comments: 0

∫ (dx/((1−sinx)^2 )) ?

$$\int\:\frac{{dx}}{\left(\mathrm{1}−{sinx}\right)^{\mathrm{2}} }\:? \\ $$

Question Number 103826 Answers: 1 Comments: 0

In the expansion of (1+x)^(20) if the coefficient of x^r is twice the coefficient of x^(r−1) , what the value of the coefficient?

$${In}\:{the}\:{expansion}\:{of}\:\left(\mathrm{1}+{x}\right)^{\mathrm{20}} \:{if}\:{the} \\ $$$${coefficient}\:{of}\:{x}^{{r}} \:{is}\:{twice}\:{the}\:{coefficient} \\ $$$${of}\:{x}^{{r}−\mathrm{1}} ,\:{what}\:{the}\:{value}\:{of}\:{the} \\ $$$${coefficient}?\: \\ $$

Question Number 103823 Answers: 2 Comments: 0

tan (x) = 4 cos (2x)−cot (2x)

$$\mathrm{tan}\:\left({x}\right)\:=\:\mathrm{4}\:\mathrm{cos}\:\left(\mathrm{2}{x}\right)−\mathrm{cot}\:\left(\mathrm{2}{x}\right) \\ $$

Question Number 103820 Answers: 1 Comments: 0

∫_R ^ (e^(−2iπax) /((1+x^2 )^2 ))dx = πe^(−2πa) ((1/2)+πa) a>0

$$\:\:\:\int_{\mathbb{R}} ^{} \:\frac{{e}^{−\mathrm{2}{i}\pi{ax}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:=\:\pi{e}^{−\mathrm{2}\pi{a}} \left(\frac{\mathrm{1}}{\mathrm{2}}+\pi{a}\right)\:\:\:\:\:\:\:\:\:{a}>\mathrm{0} \\ $$

Question Number 103887 Answers: 1 Comments: 3

how do you prove sin (a+b) = sin a cos b + cos a sin b geometrically ?

$${how}\:{do}\:{you}\:{prove}\:\mathrm{sin}\:\left({a}+{b}\right)\:=\:\mathrm{sin} \\ $$$${a}\:\mathrm{cos}\:{b}\:+\:\mathrm{cos}\:{a}\:\mathrm{sin}\:{b} \\ $$$${geometrically}\:? \\ $$

Question Number 103804 Answers: 0 Comments: 0

Solve for r ((h−p^2 )/(p−r))=(1/(2p)) , ((h−q)/(q^2 −r))= 2q (h−p^2 )^2 +(p−r)^2 =r^2 (h−q)^2 +(q^2 −r)^2 =r^2

$$\:\:\:\boldsymbol{{S}}{olve}\:{for}\:\boldsymbol{{r}} \\ $$$$\:\:\frac{\boldsymbol{{h}}−\boldsymbol{{p}}^{\mathrm{2}} }{\boldsymbol{{p}}−\boldsymbol{{r}}}=\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{p}}}\:\:\:\:,\:\:\:\:\frac{\boldsymbol{{h}}−\boldsymbol{{q}}}{\boldsymbol{{q}}^{\mathrm{2}} −\boldsymbol{{r}}}=\:\mathrm{2}\boldsymbol{{q}} \\ $$$$\left(\boldsymbol{{h}}−\boldsymbol{{p}}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\boldsymbol{{p}}−\boldsymbol{{r}}\right)^{\mathrm{2}} =\boldsymbol{{r}}^{\mathrm{2}} \\ $$$$\:\left(\boldsymbol{{h}}−\boldsymbol{{q}}\right)^{\mathrm{2}} +\left(\boldsymbol{{q}}^{\mathrm{2}} −\boldsymbol{{r}}\right)^{\mathrm{2}} =\boldsymbol{{r}}^{\mathrm{2}} \\ $$

Question Number 103792 Answers: 2 Comments: 0

Question Number 103790 Answers: 1 Comments: 1

Pg 1139 Pg 1140 Pg 1141 Pg 1142 Pg 1143 Pg 1144 Pg 1145 Pg 1146 Pg 1147 Pg 1148

Terms of Service

Contact: [email protected]