Question and Answers Forum

AllQuestion and Answers: Page 1142

Question Number 104197 Answers: 2 Comments: 0

calculate ∫_5 ^(+∞) (dx/((x^2 −9)^4 ))

$$\mathrm{calculate}\:\int_{\mathrm{5}} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{4}} } \\ $$

Question Number 104201 Answers: 0 Comments: 0

If a^2 + b^2 + c^2 = 1 and b + ic = (1 + a)z, then show that ((a + ib)/(i + c)) = ((1 + iz)/(1 − iz))

$$\mathrm{If}\:\:\:\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \:+\:\mathrm{c}^{\mathrm{2}} \:\:=\:\:\mathrm{1}\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\mathrm{b}\:\:+\:\:\mathrm{ic}\:\:=\:\:\left(\mathrm{1}\:\:+\:\:\mathrm{a}\right)\mathrm{z}, \\ $$$$\mathrm{then}\:\mathrm{show}\:\mathrm{that}\:\:\:\:\:\:\frac{\mathrm{a}\:\:+\:\:\mathrm{ib}}{\mathrm{i}\:\:+\:\:\mathrm{c}}\:\:\:=\:\:\:\frac{\mathrm{1}\:\:+\:\:\mathrm{iz}}{\mathrm{1}\:\:−\:\:\mathrm{iz}} \\ $$

Question Number 104191 Answers: 1 Comments: 0

Given (E):x^4 −10x^2 +q=0 U=x^2 so (E_((U)) )=U^2 −40U+q=0 . We suppose that E_((U)) has two roots such as r_1 <r_(2 ) . We give also that r_1 +r_2 =40 and r_1 ×r_2 =q. 1)The equation E has four positive solution. Determinate them such that these solutions form an arithmetical progression.

$${Given}\:\left({E}\right):{x}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{2}} +{q}=\mathrm{0} \\ $$$${U}={x}^{\mathrm{2}} \:{so}\:\left({E}_{\left({U}\right)} \right)={U}^{\mathrm{2}} −\mathrm{40}{U}+{q}=\mathrm{0}\:. \\ $$$${We}\:{suppose}\:{that}\:{E}_{\left({U}\right)} {has}\:{two}\:{roots} \\ $$$${such}\:{as}\:{r}_{\mathrm{1}} <{r}_{\mathrm{2}\:} . \\ $$$${We}\:{give}\:{also}\:{that}\:{r}_{\mathrm{1}} +{r}_{\mathrm{2}} =\mathrm{40}\:{and} \\ $$$${r}_{\mathrm{1}} ×{r}_{\mathrm{2}} ={q}. \\ $$$$\left.\mathrm{1}\right){The}\:{equation}\:{E}\:{has}\:{four}\:{positive} \\ $$$${solution}.\:{Determinate}\:{them}\:{such} \\ $$$${that}\:{these}\:{solutions}\:{form}\:{an}\: \\ $$$${arithmetical}\:{progression}. \\ $$$$ \\ $$

Question Number 104190 Answers: 3 Comments: 1

integers x,y satisfy 2x+15y=2019. find the minimum of ∣y−x∣.

$${integers}\:{x},{y}\:{satisfy}\:\mathrm{2}{x}+\mathrm{15}{y}=\mathrm{2019}. \\ $$$${find}\:{the}\:{minimum}\:{of}\:\mid{y}−{x}\mid. \\ $$

Question Number 104187 Answers: 2 Comments: 0

Given: (E): (m+1)x^2 +(m−2)x+1=0 We suppose that it has two roots x_1 and x_2 . Determinate m such that: x_1 =1+x_2

$${Given}: \\ $$$$\left({E}\right):\:\left({m}+\mathrm{1}\right){x}^{\mathrm{2}} +\left({m}−\mathrm{2}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$${We}\:{suppose}\:{that}\:{it}\:{has}\:{two}\:{roots}\:{x}_{\mathrm{1}} \\ $$$${and}\:{x}_{\mathrm{2}} . \\ $$$${Determinate}\:{m}\:{such}\:{that}: \\ $$$${x}_{\mathrm{1}} =\mathrm{1}+{x}_{\mathrm{2}} \\ $$

Question Number 104181 Answers: 1 Comments: 0

Given P(x)=x^4 +2x^3 −41x^2 +42x+360 Determinate Q(x) a quadratic poly− nom such that: P(x)=(Q(x))^2 −42(Q(x))+360

$${Given} \\ $$$${P}\left({x}\right)={x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{41}{x}^{\mathrm{2}} +\mathrm{42}{x}+\mathrm{360} \\ $$$${Determinate}\:{Q}\left({x}\right)\:{a}\:{quadratic}\:{poly}− \\ $$$${nom}\:{such}\:{that}: \\ $$$${P}\left({x}\right)=\left({Q}\left({x}\right)\right)^{\mathrm{2}} −\mathrm{42}\left({Q}\left({x}\right)\right)+\mathrm{360} \\ $$

Question Number 104180 Answers: 0 Comments: 0

Question Number 104178 Answers: 3 Comments: 0

Solve in R a) 3∣x−(√3)∣−8(√((∣x−(√3)∣)+4))=0 b)(√((∣x^2 −x−6))∣)=x+1 c)(√((x^3 −27))+6<x+3

$${Solve}\:{in}\:\mathbb{R} \\ $$$$\left.{a}\right)\:\mathrm{3}\mid{x}−\sqrt{\mathrm{3}}\mid−\mathrm{8}\sqrt{\left(\mid{x}−\sqrt{\mathrm{3}}\mid\right)+\mathrm{4}}=\mathrm{0} \\ $$$$\left.{b}\left.\right)\sqrt{\left(\mid{x}^{\mathrm{2}} −{x}−\mathrm{6}\right.}\mid\right)={x}+\mathrm{1} \\ $$$$\left.{c}\right)\sqrt{\left({x}^{\mathrm{3}} −\mathrm{27}\right.}+\mathrm{6}<{x}+\mathrm{3} \\ $$

Question Number 104174 Answers: 2 Comments: 0

Π_(n=1) ^∞ ((n/(n+1)))^2

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$

Question Number 104173 Answers: 0 Comments: 0

For fun! S_n =1+2+3+4+5+6+7+... 2S_n = 2 + 4 + 6 +.. −S_n =1+3+5+7+9+11+..... −(−(1/(12)))=1+3+5+7+9+11+... 1+3+5+7+9+....=(1/(12)) S_n =1+2+3+4+5+6+7+.... S_n =1+(1+1)+(1+2)+(1+3)+... S_n =(1+1+1+....)+S_n 1+1+1+1+1+1+....=0

$$\:\mathrm{For}\:\mathrm{fun}! \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+... \\ $$$$\mathrm{2S}_{\mathrm{n}} =\:\:\:\:\mathrm{2}\:\:+\:\:\:\mathrm{4}\:\:\:\:\:\:+\:\:\mathrm{6}\:\:\:\:\:\:+.. \\ $$$$−\mathrm{S}_{\mathrm{n}} =\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+\mathrm{9}+\mathrm{11}+..... \\ $$$$−\left(−\frac{\mathrm{1}}{\mathrm{12}}\right)=\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+\mathrm{9}+\mathrm{11}+... \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+\mathrm{9}+....=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$ \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+.... \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{1}+\left(\mathrm{1}+\mathrm{1}\right)+\left(\mathrm{1}+\mathrm{2}\right)+\left(\mathrm{1}+\mathrm{3}\right)+... \\ $$$$\mathrm{S}_{\mathrm{n}} =\left(\mathrm{1}+\mathrm{1}+\mathrm{1}+....\right)+\mathrm{S}_{\mathrm{n}} \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+....=\mathrm{0} \\ $$

Question Number 104171 Answers: 0 Comments: 1

App Updates: v2.110 is available now on www.tinkutara.com and will be available in playstore in a day. This version improves drawing: − sidebar buttons are added − Multiple shape selection for alignment can be done from sidebar. − A new polyline option is added so a free handline can be drawn by tapping point. While in polyline mode arrow key can be used to adjust last point.

$$\mathrm{App}\:\mathrm{Updates}: \\ $$$$\mathrm{v2}.\mathrm{110}\:\mathrm{is}\:\mathrm{available}\:\mathrm{now}\:\mathrm{on} \\ $$$$\mathrm{www}.\mathrm{tinkutara}.\mathrm{com}\:\mathrm{and}\:\mathrm{will}\:\mathrm{be} \\ $$$$\mathrm{available}\:\mathrm{in}\:\mathrm{playstore}\:\mathrm{in}\:\mathrm{a}\:\mathrm{day}. \\ $$$$\mathrm{This}\:\mathrm{version}\:\mathrm{improves}\:\mathrm{drawing}: \\ $$$$−\:\mathrm{sidebar}\:\mathrm{buttons}\:\mathrm{are}\:\mathrm{added} \\ $$$$−\:\mathrm{Multiple}\:\mathrm{shape}\:\mathrm{selection}\:\mathrm{for} \\ $$$$\:\:\:\:\:\mathrm{alignment}\:\mathrm{can}\:\mathrm{be}\:\mathrm{done}\:\mathrm{from} \\ $$$$\mathrm{sidebar}. \\ $$$$−\:\mathrm{A}\:\mathrm{new}\:\mathrm{polyline}\:\mathrm{option}\:\mathrm{is}\:\mathrm{added} \\ $$$$\:\:\:\:\:\mathrm{so}\:\mathrm{a}\:\mathrm{free}\:\mathrm{handline}\:\mathrm{can}\:\mathrm{be}\:\mathrm{drawn} \\ $$$$\:\:\:\:\:\mathrm{by}\:\mathrm{tapping}\:\mathrm{point}.\:\mathrm{While}\:\mathrm{in} \\ $$$$\:\:\:\:\:\mathrm{polyline}\:\mathrm{mode}\:\mathrm{arrow}\:\mathrm{key}\:\mathrm{can}\:\mathrm{be} \\ $$$$\:\:\:\:\:\mathrm{used}\:\mathrm{to}\:\mathrm{adjust}\:\mathrm{last}\:\mathrm{point}. \\ $$

Question Number 104165 Answers: 0 Comments: 1

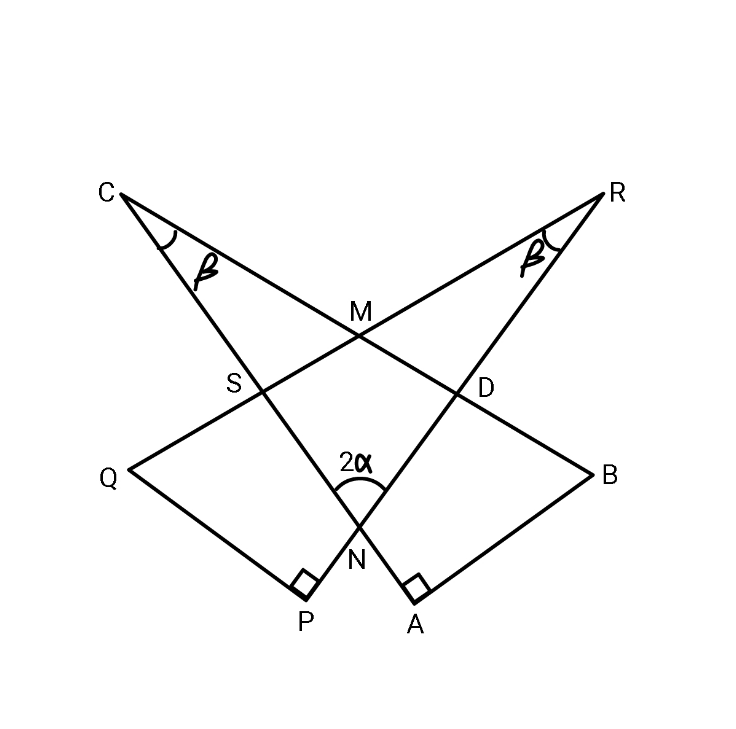
Question Number 104157 Answers: 2 Comments: 1

Question Number 104155 Answers: 0 Comments: 3

Question Number 104134 Answers: 2 Comments: 0

what is the coefficient x^(15) in the expansion of x^6 (1−x)^(11)

$${what}\:{is}\:{the}\:{coefficient}\:{x}^{\mathrm{15}} \\ $$$${in}\:{the}\:{expansion}\:{of}\:{x}^{\mathrm{6}} \left(\mathrm{1}−{x}\right)^{\mathrm{11}} \\ $$

Question Number 104132 Answers: 0 Comments: 0

what is the solution D^4 y = 12x by the variation of parameters

$${what}\:{is}\:{the}\:{solution}\: \\ $$$${D}^{\mathrm{4}} {y}\:=\:\mathrm{12}{x}\:{by}\:{the}\:{variation}\: \\ $$$${of}\:{parameters}\: \\ $$

Question Number 104141 Answers: 1 Comments: 0

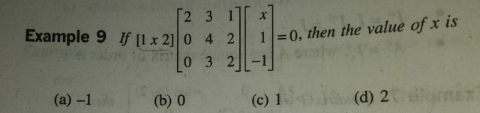
Question Number 104139 Answers: 2 Comments: 1

what is remainder when 61^(61) divided by 1001

$${what}\:{is}\:{remainder}\:{when}\:\mathrm{61}^{\mathrm{61}} \:{divided} \\ $$$${by}\:\mathrm{1001} \\ $$

Question Number 104122 Answers: 1 Comments: 0

(1/(sin2x))+(1/(sin2^2 x))+.....+(1/(sin2^n x)) Find the value

$$\frac{\mathrm{1}}{\mathrm{sin2x}}+\frac{\mathrm{1}}{\mathrm{sin2}^{\mathrm{2}} \mathrm{x}}+.....+\frac{\mathrm{1}}{\mathrm{sin2}^{\mathrm{n}} \mathrm{x}} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\: \\ $$

Question Number 104115 Answers: 1 Comments: 0

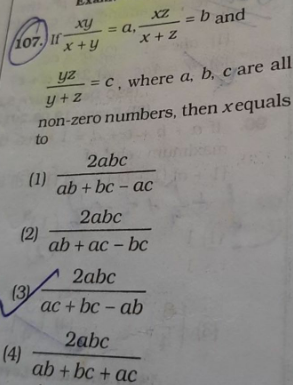
Question Number 104110 Answers: 1 Comments: 0

in a box A there are 3 red balls and 2 white balls.while in box B there are 4 red balls and 5 white balls.if from boxA and B each are taken two balls one by one with return . the chance of being taken is one white ball? a.(4/(675)) c.((128)/(675)) e.((218)/(675)) b.((64)/(675)) d.((184)/(675))

$${in}\:{a}\:{box}\:{A}\:{there}\:{are}\:\mathrm{3}\:{red}\:{balls}\:{and}\:\mathrm{2}\:{white} \\ $$$${balls}.{while}\:{in}\:{box}\:{B}\:{there}\:{are}\:\mathrm{4}\:{red}\:{balls}\:{and} \\ $$$$\mathrm{5}\:{white}\:{balls}.{if}\:{from}\:{boxA}\:{and}\:{B}\:{each}\:{are}\: \\ $$$${taken}\:{two}\:{balls}\:{one}\:{by}\:{one}\:{with}\:{return}\:.\:{the}\: \\ $$$${chance}\:{of}\:{being}\:{taken}\:{is}\:{one}\:{white}\:{ball}? \\ $$$${a}.\frac{\mathrm{4}}{\mathrm{675}}\:\:\:\:\:{c}.\frac{\mathrm{128}}{\mathrm{675}}\:\:\:\:\:\:{e}.\frac{\mathrm{218}}{\mathrm{675}} \\ $$$${b}.\frac{\mathrm{64}}{\mathrm{675}}\:\:\:\:\:\:{d}.\frac{\mathrm{184}}{\mathrm{675}} \\ $$$$ \\ $$$$ \\ $$

Question Number 104101 Answers: 1 Comments: 2

Question Number 104100 Answers: 3 Comments: 0

(1)Find all natural pairs of integers (x,y) such that x^3 −y^3 =xy+61. (2)Find gcd(x^4 −x^3 , x^3 −x)

$$\left(\mathrm{1}\right)\mathbb{F}{ind}\:{all}\:{natural}\:{pairs}\:{of} \\ $$$${integers}\:\left({x},{y}\right)\:{such}\:{that}\:{x}^{\mathrm{3}} −{y}^{\mathrm{3}} ={xy}+\mathrm{61}. \\ $$$$\left(\mathrm{2}\right)\mathbb{F}{ind}\:{gcd}\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} ,\:{x}^{\mathrm{3}} −{x}\right)\: \\ $$

Question Number 104099 Answers: 0 Comments: 0

Question Number 104333 Answers: 2 Comments: 0

if i^( 5n +1 ) = 1 , n∈Z then show that : n = 3+4p ,p∈Z

$${if}\:{i}^{\:\mathrm{5}{n}\:+\mathrm{1}\:} =\:\mathrm{1}\:\:\:\:,\:{n}\in{Z} \\ $$$${then}\:{show}\:{that}\::\:{n}\:=\:\mathrm{3}+\mathrm{4}{p}\:\:\:,{p}\in{Z} \\ $$

Question Number 104093 Answers: 2 Comments: 0

(1)Evaluate the sum ⌊(2^0 /3)⌋+⌊(2^1 /3)⌋+⌊(2^2 /3)⌋+...+⌊(2^(1000) /3)⌋ (2) find 2^(98) (mod 33)

$$\left(\mathrm{1}\right){Evaluate}\:{the}\:{sum}\:\lfloor\frac{\mathrm{2}^{\mathrm{0}} }{\mathrm{3}}\rfloor+\lfloor\frac{\mathrm{2}^{\mathrm{1}} }{\mathrm{3}}\rfloor+\lfloor\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}}\rfloor+...+\lfloor\frac{\mathrm{2}^{\mathrm{1000}} }{\mathrm{3}}\rfloor \\ $$$$\left(\mathrm{2}\right)\:{find}\:\mathrm{2}^{\mathrm{98}} \:\left({mod}\:\mathrm{33}\right)\: \\ $$

Pg 1137 Pg 1138 Pg 1139 Pg 1140 Pg 1141 Pg 1142 Pg 1143 Pg 1144 Pg 1145 Pg 1146

Contact: [email protected]