Question and Answers Forum

AllQuestion and Answers: Page 1139

Question Number 104060 Answers: 1 Comments: 0

evaluate ∫∫_s (xz+y^2 )dS where S is the surface described by x^2 +y^2 =16 , 0≤z≤3

$${evaluate}\:\int\int_{{s}} \left({xz}+{y}^{\mathrm{2}} \right){dS}\:{where} \\ $$$${S}\:{is}\:{the}\:{surface}\:{described}\:{by}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{16} \\ $$$$,\:\mathrm{0}\leqslant{z}\leqslant\mathrm{3} \\ $$

Question Number 104159 Answers: 0 Comments: 3

How may we plot the graph of f(x)=x+(√((x(x+2))/(x+1))) , with the help of a variation table ?

$$\mathrm{How}\:\mathrm{may}\:\mathrm{we}\:\mathrm{plot}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{of} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}+\sqrt{\frac{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}{\mathrm{x}+\mathrm{1}}}\:,\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{a}\:\mathrm{variation}\:\mathrm{table}\:? \\ $$

Question Number 104051 Answers: 3 Comments: 0

(x^2 −1) (dy/dx) + 2y = (x+1)^2

$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\:\frac{{dy}}{{dx}}\:+\:\mathrm{2}{y}\:=\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$

Question Number 104046 Answers: 0 Comments: 6

To do normally his commercial activities in some place situated at 150km from him, a driver use a car. the consumption of gazoil in liters for 10 km is defined by: C(v)=((20)/v)+(v/(45)) where v is the speed of car. How should be the speed of car to reduce minimally the consumption of gazoil?

$$\mathrm{To}\:\mathrm{do}\:\mathrm{normally}\:\mathrm{his}\:\mathrm{commercial} \\ $$$$\mathrm{activities}\:\mathrm{in}\:\mathrm{some}\:\mathrm{place}\:\mathrm{situated}\:\mathrm{at}\:\mathrm{150km} \\ $$$$\mathrm{from}\:\mathrm{him},\:\mathrm{a}\:\mathrm{driver}\:\mathrm{use}\:\mathrm{a}\:\mathrm{car}.\:\mathrm{the}\:\mathrm{consumption} \\ $$$$\mathrm{of}\:\mathrm{gazoil}\:\mathrm{in}\:\mathrm{liters}\:\mathrm{for}\:\mathrm{10}\:\mathrm{km}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{by}: \\ $$$$\mathrm{C}\left(\mathrm{v}\right)=\frac{\mathrm{20}}{\mathrm{v}}+\frac{\mathrm{v}}{\mathrm{45}}\:\mathrm{where}\:\mathrm{v}\:\mathrm{is}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{car}. \\ $$$$\mathrm{How}\:\mathrm{should}\:\mathrm{be}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{car}\:\mathrm{to}\:\mathrm{reduce} \\ $$$$\mathrm{minimally}\:\mathrm{the}\:\mathrm{consumption}\:\mathrm{of}\:\mathrm{gazoil}? \\ $$

Question Number 104038 Answers: 1 Comments: 0

what is the largest positive integer n such that n^3 +100 is divisible by n+10 ?

$${what}\:{is}\:{the}\:{largest}\:{positive} \\ $$$${integer}\:{n}\:{such}\:{that}\:{n}^{\mathrm{3}} +\mathrm{100}\:{is} \\ $$$${divisible}\:{by}\:{n}+\mathrm{10}\:?\: \\ $$

Question Number 104037 Answers: 4 Comments: 0

(1) { ((x^3 +y^6 = 91)),((x+y^2 = 7 )) :} find x−y^6 . (2) 2a+(2/a) = 8 ⇒ ((a^6 +1)/a^3 ) ?

$$\left(\mathrm{1}\right)\begin{cases}{{x}^{\mathrm{3}} +{y}^{\mathrm{6}} \:=\:\mathrm{91}}\\{{x}+{y}^{\mathrm{2}} \:=\:\mathrm{7}\:}\end{cases} \\ $$$${find}\:{x}−{y}^{\mathrm{6}} \:. \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2}{a}+\frac{\mathrm{2}}{{a}}\:=\:\mathrm{8}\:\Rightarrow\:\frac{{a}^{\mathrm{6}} +\mathrm{1}}{{a}^{\mathrm{3}} }\:? \\ $$

Question Number 104035 Answers: 1 Comments: 0

Find the image of point OP^(→) = p^ in the line r^ =a^ +λb^ .

$${Find}\:{the}\:{image}\:{of}\:{point}\:\overset{\rightarrow} {{OP}}\:=\:\bar {{p}}\:\:{in} \\ $$$${the}\:{line}\:\:\bar {{r}}=\bar {{a}}+\lambda\bar {{b}}\:. \\ $$

Question Number 104034 Answers: 2 Comments: 0

Solve: y^(′′) +2y^′ +2y=secax

$${Solve}:\:{y}^{''} +\mathrm{2}{y}^{'} +\mathrm{2}{y}={secax} \\ $$

Question Number 104028 Answers: 2 Comments: 0

calculate ∫_(20) ^(+∞) (dx/((x−18)^(19) (x−19)^(18) ))

$$\mathrm{calculate}\:\:\int_{\mathrm{20}} ^{+\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{18}\right)^{\mathrm{19}} \left(\mathrm{x}−\mathrm{19}\right)^{\mathrm{18}} } \\ $$

Question Number 104016 Answers: 1 Comments: 0

Question Number 104023 Answers: 0 Comments: 1

Question Number 103998 Answers: 3 Comments: 5

if f(x)=x^(3/2) f′(0)=0 or not exist

$${if}\:\:\:\:{f}\left({x}\right)={x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${f}'\left(\mathrm{0}\right)=\mathrm{0}\:\:{or}\:{not}\:{exist} \\ $$

Question Number 103986 Answers: 1 Comments: 1

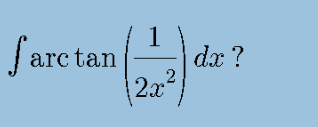
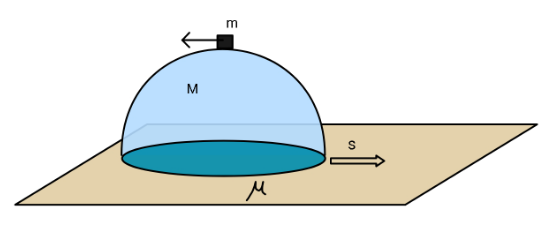
Question Number 103983 Answers: 0 Comments: 0

If α and β are two unequal angle, which satisfy the equation, a cos(α) + b sin(β) = c, show that (i) sin(((α + β)/2)) sec(((α − β)/2)) = (b/c) (ii) tan((α/2)) tan((β/2)) = ((c − a)/(c + a))

$$\mathrm{If}\:\:\alpha\:\:\mathrm{and}\:\:\beta\:\:\mathrm{are}\:\mathrm{two}\:\mathrm{unequal}\:\mathrm{angle},\:\mathrm{which}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation}, \\ $$$$\:\:\:\:\mathrm{a}\:\mathrm{cos}\left(\alpha\right)\:\:+\:\:\mathrm{b}\:\mathrm{sin}\left(\beta\right)\:\:=\:\:\mathrm{c},\:\:\:\:\mathrm{show}\:\mathrm{that} \\ $$$$\left(\mathrm{i}\right)\:\:\:\:\mathrm{sin}\left(\frac{\alpha\:\:+\:\beta}{\mathrm{2}}\right)\:\mathrm{sec}\left(\frac{\alpha\:\:−\:\:\beta}{\mathrm{2}}\right)\:\:=\:\:\frac{\mathrm{b}}{\mathrm{c}} \\ $$$$\left(\mathrm{ii}\right)\:\:\:\:\:\mathrm{tan}\left(\frac{\alpha}{\mathrm{2}}\right)\:\mathrm{tan}\left(\frac{\beta}{\mathrm{2}}\right)\:\:=\:\:\frac{\mathrm{c}\:\:−\:\:\mathrm{a}}{\mathrm{c}\:\:+\:\:\mathrm{a}} \\ $$

Question Number 103984 Answers: 0 Comments: 1

tan^2 (x)+tan^2 (2x)+tan^2 (4x)=33 x=?

$$\:\:\:\:\boldsymbol{{tan}}^{\mathrm{2}} \left(\boldsymbol{{x}}\right)+\boldsymbol{{tan}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{{x}}\right)+\boldsymbol{{tan}}^{\mathrm{2}} \left(\mathrm{4}\boldsymbol{{x}}\right)=\mathrm{33} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{x}}=? \\ $$

Question Number 103979 Answers: 0 Comments: 1

show right and left sid limitation of lim_(x→0) ((ln(b−x))/(ax))

$$\:\:{show}\:{right}\:{and}\:{left}\:{sid}\:\:\:\:{limitation}\:\:\:\: \\ $$$${of}\:\:\:{li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{{ln}\left({b}−{x}\right)}{{ax}} \\ $$$$ \\ $$

Question Number 103974 Answers: 2 Comments: 0

calculate ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +3)^2 ))

$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} } \\ $$

Question Number 103969 Answers: 1 Comments: 0

how do you solve (D^3 +12D^2 +36D)y=0 by constant coefficients

$${how}\:{do}\:{you}\:{solve}\:\left({D}^{\mathrm{3}} +\mathrm{12}{D}^{\mathrm{2}} +\mathrm{36}{D}\right){y}=\mathrm{0} \\ $$$${by}\:{constant}\:{coefficients} \\ $$

Question Number 103961 Answers: 3 Comments: 0

what is 2^(log2x) =3^(log3x)

$${what}\:{is}\: \\ $$$$\mathrm{2}^{{log}\mathrm{2}{x}} =\mathrm{3}^{{log}\mathrm{3}{x}} \\ $$

Question Number 103958 Answers: 1 Comments: 0

what is integrating factor of (xy^2 −y) dx − x dy = 0

$${what}\:{is}\:{integrating}\:{factor} \\ $$$${of}\:\left({xy}^{\mathrm{2}} −{y}\right)\:{dx}\:−\:{x}\:{dy}\:=\:\mathrm{0} \\ $$

Question Number 103945 Answers: 2 Comments: 0

a cube ABCD.EFGH with length side 4 cm. Given point P is midpoint EF. find the distance of line AP to line HB.

$${a}\:{cube}\:{ABCD}.{EFGH}\:{with}\:{length}\:{side} \\ $$$$\mathrm{4}\:{cm}.\:{Given}\:{point}\:{P}\:{is}\:{midpoint}\:{EF}. \\ $$$${find}\:{the}\:{distance}\:{of}\:{line}\:{AP}\:{to}\:{line} \\ $$$${HB}.\: \\ $$

Question Number 103931 Answers: 2 Comments: 0

(y^2 +2) dx = (xy+2y+y^3 ) dy

$$\left({y}^{\mathrm{2}} +\mathrm{2}\right)\:{dx}\:=\:\left({xy}+\mathrm{2}{y}+{y}^{\mathrm{3}} \right)\:{dy} \\ $$

Question Number 103928 Answers: 1 Comments: 0

Question Number 103921 Answers: 1 Comments: 0

Prove that ∀ x ∈ R^ , ∣ cos x ∣ ≤ 1 − sin^2 x

$$\mathrm{Prove}\:\mathrm{that}\:\forall\:{x}\:\in\:\bar {\mathbb{R}}\:,\:\mid\:\mathrm{cos}\:{x}\:\mid\:\leqslant\:\mathrm{1}\:−\:\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$

Question Number 103914 Answers: 2 Comments: 2

(2+(√3))^x^2 + (2−(√3))^x^2 = 4

$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}^{\mathrm{2}} } \:+\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{{x}^{\mathrm{2}} } \:=\:\mathrm{4}\: \\ $$

Question Number 103908 Answers: 2 Comments: 2

Find the least positive integer n for which there exists a set { s_1 ,s_2 ,s_3 ,...,s_n } consisting of n distinct positive integers such that (1−(1/s_1 ))(1−(1/s_2 ))(1−(1/s_3 ))...(1−(1/s_n )) = ((51)/(2010)) .

$${Find}\:{the}\:{least}\:{positive}\:{integer}\:{n}\:{for} \\ $$$${which}\:{there}\:{exists}\:{a}\:{set}\:\left\{\:{s}_{\mathrm{1}} ,{s}_{\mathrm{2}} ,{s}_{\mathrm{3}} ,...,{s}_{{n}} \:\right\} \\ $$$${consisting}\:{of}\:{n}\:{distinct}\:{positive}\:{integers} \\ $$$${such}\:{that}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{1}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{\mathrm{3}} }\right)...\left(\mathrm{1}−\frac{\mathrm{1}}{{s}_{{n}} }\right) \\ $$$$=\:\frac{\mathrm{51}}{\mathrm{2010}}\:. \\ $$

Pg 1134 Pg 1135 Pg 1136 Pg 1137 Pg 1138 Pg 1139 Pg 1140 Pg 1141 Pg 1142 Pg 1143

Contact: info@tinkutara.com