Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1128

Question Number 105380 Answers: 1 Comments: 1

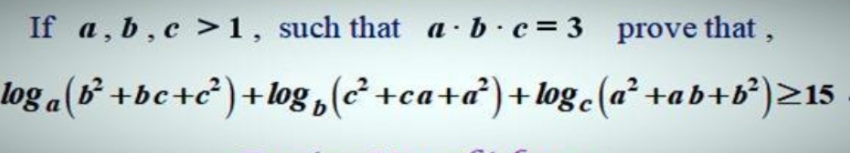
Question Number 105366 Answers: 1 Comments: 0

Question Number 105370 Answers: 4 Comments: 0

Question Number 105361 Answers: 0 Comments: 0

solve by Frobenius method x^2 y′′−x(2x−1)y′+(x+1)y=0

$${solve}\:{by}\:{Frobenius}\:{method} \\ $$$${x}^{\mathrm{2}} {y}''−{x}\left(\mathrm{2}{x}−\mathrm{1}\right){y}'+\left({x}+\mathrm{1}\right){y}=\mathrm{0} \\ $$

Question Number 105356 Answers: 1 Comments: 0

Given a cube ABCD.EFGH. if α is the angle BEH & BEG , find the value of cos α ?

$$\mathcal{G}{iven}\:{a}\:{cube}\:{ABCD}.{EFGH}. \\ $$$${if}\:\alpha\:{is}\:{the}\:{angle}\:{BEH}\:\&\:{BEG}\:, \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{cos}\:\alpha\:? \\ $$

Question Number 105353 Answers: 0 Comments: 0

solve y^(′′ ) +2y^′ −y =x^n e^(−x) n integr natural

$${solve}\:{y}^{''\:} +\mathrm{2}{y}^{'} −{y}\:={x}^{{n}} \:{e}^{−{x}} \\ $$$${n}\:{integr}\:{natural} \\ $$

Question Number 105340 Answers: 1 Comments: 0

1\Show that the polynomial, P(x)=x^n +ax+b, n≥2 (a,b)∈R^2 has at most 3 real distinct roots. 2\Show that the equation x^4 +4ax+b=0 has no more than 2 real distinct roots.

$$\mathrm{1}\backslash\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{polynomial},\:\mathrm{P}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{n}} +\mathrm{ax}+\mathrm{b},\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\left(\mathrm{a},\mathrm{b}\right)\in\mathbb{R}^{\mathrm{2}} \:\mathrm{has}\:\mathrm{at}\:\mathrm{most}\:\mathrm{3}\:\mathrm{real}\:\mathrm{distinct}\:\mathrm{roots}. \\ $$$$\mathrm{2}\backslash\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{4}} +\mathrm{4ax}+\mathrm{b}=\mathrm{0}\:\mathrm{has}\:\mathrm{no} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{2}\:\mathrm{real}\:\mathrm{distinct}\:\mathrm{roots}. \\ $$

Question Number 105331 Answers: 0 Comments: 3

lim_(t→0) (1/t)ln[1−((ln(1+t))/(ln(t)))]

$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{t}}\mathrm{ln}\left[\mathrm{1}−\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{ln}\left(\mathrm{t}\right)}\right] \\ $$

Question Number 105327 Answers: 2 Comments: 3

If x = ((11)/8) and y = ((66)/9) then what is the answer of ((x+y)/(x−y)) ?

$$\mathrm{If}\:\mathrm{x}\:=\:\frac{\mathrm{11}}{\mathrm{8}}\:\mathrm{and}\:\mathrm{y}\:=\:\frac{\mathrm{66}}{\mathrm{9}}\:\mathrm{then}\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{of}\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\:?\: \\ $$

Question Number 105322 Answers: 0 Comments: 1

Question Number 105320 Answers: 0 Comments: 0

find C kx^2 +ky^2 +z^2 ≥C x,y,z,k∈R such that xy+yz+zx=1

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{C}} \\ $$$${kx}^{\mathrm{2}} +{ky}^{\mathrm{2}} +{z}^{\mathrm{2}} \geqslant{C} \\ $$$${x},{y},{z},{k}\in\mathbb{R}\:\:{such}\:{that} \\ $$$${xy}+{yz}+{zx}=\mathrm{1} \\ $$

Question Number 105234 Answers: 0 Comments: 0

f:R→R x,y∈R f(f(x)f(y))+f(x+y)=f(xy) f(x)=?

$${f}:\mathbb{R}\rightarrow\mathbb{R}\:\:{x},{y}\in\mathbb{R} \\ $$$${f}\left({f}\left({x}\right){f}\left({y}\right)\right)+{f}\left({x}+{y}\right)={f}\left({xy}\right) \\ $$$${f}\left({x}\right)=? \\ $$

Question Number 105233 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((ch(cosx)−cos(chx))/(x^2 +3))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ch}\left(\mathrm{cosx}\right)−\mathrm{cos}\left(\mathrm{chx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}}\mathrm{dx} \\ $$

Question Number 105232 Answers: 1 Comments: 0

calculate ∫_0 ^∞ ((cos(2x^2 ))/((4x^2 +9)^3 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{2x}^{\mathrm{2}} \right)}{\left(\mathrm{4x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$

Question Number 105231 Answers: 1 Comments: 0

calculate ∫_0 ^(+∞) ((2x^2 −1)/((x^2 +x+1)^2 (x^2 −x+1)^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 105230 Answers: 2 Comments: 0

calculate ∫_1 ^(+∞) (dx/((x^2 +1)^2 (x^2 +4)^2 ))

$$\mathrm{calculate}\:\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} } \\ $$

Question Number 105243 Answers: 2 Comments: 0

{ ((sin 2x + sin 2y = (4/9))),((cos (x−y) = 1−sin (x+y))) :} 0 < x < (π/2) ; 0 < y < (π/2) find the value of sin (x+y) (a) −(2/3) (b) −(1/3) (c) (1/9) (d) (2/9) (e) (2/3)

$$\begin{cases}{\mathrm{sin}\:\mathrm{2}{x}\:+\:\mathrm{sin}\:\mathrm{2}{y}\:=\:\frac{\mathrm{4}}{\mathrm{9}}}\\{\mathrm{cos}\:\left({x}−{y}\right)\:=\:\mathrm{1}−\mathrm{sin}\:\left({x}+{y}\right)}\end{cases} \\ $$$$\mathrm{0}\:<\:{x}\:<\:\frac{\pi}{\mathrm{2}}\:;\:\mathrm{0}\:<\:{y}\:<\:\frac{\pi}{\mathrm{2}} \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{sin}\:\left({x}+{y}\right) \\ $$$$\left({a}\right)\:−\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\left({b}\right)\:−\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\left({c}\right)\:\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\left({d}\right)\:\frac{\mathrm{2}}{\mathrm{9}}\:\:\:\:\left({e}\right)\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Question Number 105242 Answers: 0 Comments: 0