Question and Answers Forum

f integrable continue on [a,b] let m =inf f(x) and M=sup f(x) (x ∈[a,b] prove that (b−a)^2 ≤∫_a ^b f(x)dx×∫_a ^b (dx/(f(x)))≤(((b−a)^2 )/4)(((m+M)^2 )/(mM))

$$\mathrm{f}\:\mathrm{integrable}\:\mathrm{continue}\:\mathrm{on}\:\left[\mathrm{a},\mathrm{b}\right]\:\mathrm{let}\:\mathrm{m}\:=\mathrm{inf}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{M}=\mathrm{sup}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\left(\mathrm{x}\:\in\left[\mathrm{a},\mathrm{b}\right]\:\mathrm{prove}\:\mathrm{that}\:\:\:\:\:\:\:\left(\mathrm{b}−\mathrm{a}\right)^{\mathrm{2}} \leqslant\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}×\int_{\mathrm{a}} ^{\mathrm{b}} \:\frac{\mathrm{dx}}{\mathrm{f}\left(\mathrm{x}\right)}\leqslant\frac{\left(\mathrm{b}−\mathrm{a}\right)^{\mathrm{2}} }{\mathrm{4}}\frac{\left(\mathrm{m}+\mathrm{M}\right)^{\mathrm{2}} }{\mathrm{mM}}\right. \\ $$

Question Number 107279 Answers: 1 Comments: 1

Question Number 107275 Answers: 0 Comments: 0

Question Number 107272 Answers: 1 Comments: 0

Question Number 107315 Answers: 0 Comments: 1

Question Number 107318 Answers: 1 Comments: 0

⊚bemath⊚ 6^(log _((x−1)) (((20−12x)/(x−7)))) −36 >0

$$\:\:\:\:\:\circledcirc{bemath}\circledcirc \\ $$$$\mathrm{6}^{\mathrm{log}\:_{\left({x}−\mathrm{1}\right)} \left(\frac{\mathrm{20}−\mathrm{12}{x}}{{x}−\mathrm{7}}\right)} −\mathrm{36}\:>\mathrm{0} \\ $$

Question Number 107264 Answers: 2 Comments: 1

∫_0 ^∞ ⌊(1/x^2 )⌋dx

$$\int_{\mathrm{0}} ^{\infty} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx} \\ $$

Question Number 107263 Answers: 0 Comments: 1

Σ_(n=1) ^n (√n)

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{n}} \\ $$

Question Number 107262 Answers: 0 Comments: 0

What is the requirement of last axioms i.e. 1v=v ∀ v∈V in the definition of vector space?

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{requirement}\:\mathrm{of}\:\mathrm{last} \\ $$$$\mathrm{axioms}\:\mathrm{i}.\mathrm{e}.\:\mathrm{1}{v}={v}\:\forall\:{v}\in{V}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{definition}\:\mathrm{of}\:\mathrm{vector}\:\mathrm{space}? \\ $$

Question Number 107254 Answers: 0 Comments: 1

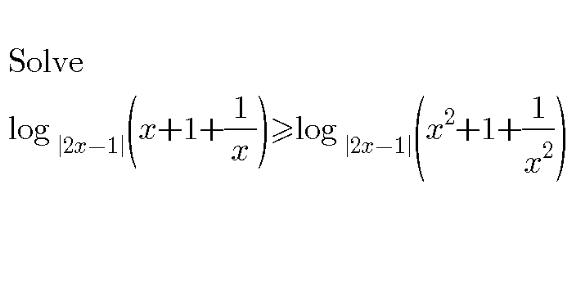
Question Number 107245 Answers: 0 Comments: 0

♣ Question♣ Why ??? ....∫_0 ^( (π/2)) (√((((2^x −1)sin^3 (x))/((2^x +1)(sin^3 (x)+cos^3 (x)))) ))<(π/8) ....M.N....

$$\:\:\:\:\:\:\:\:\clubsuit\:\mathscr{Q}{uestion}\clubsuit \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{W}{hy}\:??? \\ $$$$....\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\left(\mathrm{2}^{{x}} −\mathrm{1}\right){sin}^{\mathrm{3}} \left({x}\right)}{\left(\mathrm{2}^{{x}} +\mathrm{1}\right)\left({sin}^{\mathrm{3}} \left({x}\right)+{cos}^{\mathrm{3}} \left({x}\right)\right)}\:}<\frac{\pi}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:....\mathscr{M}.\mathscr{N}.... \\ $$

Question Number 107242 Answers: 4 Comments: 0

...question... prove that: if a,b,c∈R^+ then: ♣ (√a) +(√b)+(√c)> (√(a+b+c)) ♣ ....sincerly yours... ... M.N...

$$\:\:\:\:\:...{question}... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{prove}\:{that}: \\ $$$$\:{if}\:\:{a},{b},{c}\in\mathbb{R}^{+} \:{then}: \\ $$$$\:\:\:\:\:\clubsuit\:\:\:\sqrt{{a}}\:+\sqrt{{b}}+\sqrt{{c}}>\:\sqrt{{a}+{b}+{c}}\:\clubsuit\: \\ $$$$\:\:\:\:\:\:\:....{sincerly}\:{yours}... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:...\:\mathscr{M}.\mathscr{N}... \\ $$$$\:\: \\ $$

Question Number 107234 Answers: 1 Comments: 0

Question Number 107230 Answers: 0 Comments: 0

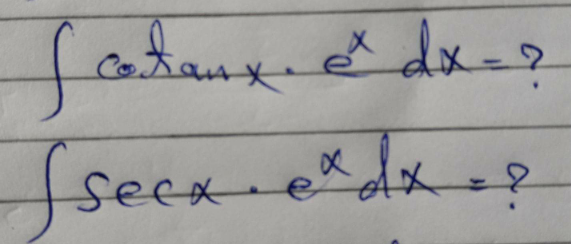
Question Number 107222 Answers: 5 Comments: 0

Question Number 107212 Answers: 4 Comments: 0

⊚bemath⊚ ∫ x^6 (√(1−x^2 )) dx ?

$$\:\:\:\circledcirc{bemath}\circledcirc \\ $$$$\int\:{x}^{\mathrm{6}} \:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:? \\ $$

Question Number 107207 Answers: 4 Comments: 0

⊚bemath⊚ lim_(x→∞) (2^x +3^x )^(1/x) ?

$$\:\:\:\:\:\circledcirc{bemath}\circledcirc \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\frac{\mathrm{1}}{{x}}} \:?\: \\ $$

Question Number 107202 Answers: 2 Comments: 0

Question Number 107238 Answers: 3 Comments: 0

⊞bemath⊞ ∫ ((sin x)/(sin^3 x+cos^3 x)) dx ?

$$\:\:\:\:\:\:\:\boxplus{bemath}\boxplus \\ $$$$\int\:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{cos}\:^{\mathrm{3}} {x}}\:{dx}\:?\: \\ $$

Question Number 107198 Answers: 1 Comments: 2

Solve the given equation: (x+(x/3^1 ))∙(x+(x/3^2 ))∙(x+(x/3^3 ))∙(x+(x/3^4 ))∙...∙(x+(x/3^(25) ))=1 A)(3^(51) /(2∙(3^(50) −1))) B)(3^(52) /(2∙(3^(51) −1))) C) (3^(50) /(2∙(3^(50) −1))) D) (3^(51) /(3^(51) −1)) Please help with solution

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}: \\ $$$$\left(\mathrm{x}+\frac{\mathrm{x}}{\mathrm{3}^{\mathrm{1}} }\right)\centerdot\left(\mathrm{x}+\frac{\mathrm{x}}{\mathrm{3}^{\mathrm{2}} }\right)\centerdot\left(\mathrm{x}+\frac{\mathrm{x}}{\mathrm{3}^{\mathrm{3}} }\right)\centerdot\left(\mathrm{x}+\frac{\mathrm{x}}{\mathrm{3}^{\mathrm{4}} }\right)\centerdot...\centerdot\left(\mathrm{x}+\frac{\mathrm{x}}{\mathrm{3}^{\mathrm{25}} }\right)=\mathrm{1} \\ $$$$\left.\mathrm{A}\left.\right)\left.\frac{\mathrm{3}^{\mathrm{51}} }{\mathrm{2}\centerdot\left(\mathrm{3}^{\mathrm{50}} −\mathrm{1}\right)}\left.\:\:\mathrm{B}\right)\frac{\mathrm{3}^{\mathrm{52}} }{\mathrm{2}\centerdot\left(\mathrm{3}^{\mathrm{51}} −\mathrm{1}\right)}\:\:\mathrm{C}\right)\:\frac{\mathrm{3}^{\mathrm{50}} }{\mathrm{2}\centerdot\left(\mathrm{3}^{\mathrm{50}} −\mathrm{1}\right)}\:\:\mathrm{D}\right)\:\frac{\mathrm{3}^{\mathrm{51}} }{\mathrm{3}^{\mathrm{51}} −\mathrm{1}} \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{solution} \\ $$

Pg 1110 Pg 1111 Pg 1112 Pg 1113 Pg 1114 Pg 1115 Pg 1116 Pg 1117 Pg 1118 Pg 1119

Contact: [email protected]