
AllQuestion and Answers: Page 1107
Question Number 108228 Answers: 3 Comments: 0
Question Number 108227 Answers: 2 Comments: 0
$$\mathrm{y}''+\mathrm{4y}'+\mathrm{5y}=\mathrm{xe}^{−\mathrm{2x}} \mathrm{sinx} \\ $$
Question Number 108264 Answers: 2 Comments: 0
Question Number 108222 Answers: 1 Comments: 0
Question Number 108219 Answers: 0 Comments: 3

Question Number 108217 Answers: 4 Comments: 1
Question Number 108208 Answers: 4 Comments: 0
Question Number 108193 Answers: 3 Comments: 1
Question Number 108181 Answers: 0 Comments: 9
Question Number 108180 Answers: 0 Comments: 0
Question Number 108175 Answers: 1 Comments: 3

Question Number 108171 Answers: 1 Comments: 0
Question Number 108169 Answers: 1 Comments: 0
Question Number 108162 Answers: 1 Comments: 0

Question Number 108158 Answers: 1 Comments: 1
$$\mathrm{test}\:\mathrm{for}\:\mathrm{edit}\:\mathrm{post}. \\ $$$${edited} \\ $$
Question Number 108145 Answers: 3 Comments: 2
Question Number 108144 Answers: 0 Comments: 0
Question Number 108143 Answers: 2 Comments: 0
Question Number 108133 Answers: 2 Comments: 1

Question Number 108131 Answers: 3 Comments: 1
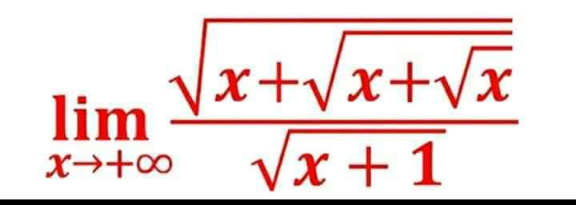
Question Number 108118 Answers: 1 Comments: 0

Question Number 108114 Answers: 1 Comments: 0

Question Number 108107 Answers: 1 Comments: 2
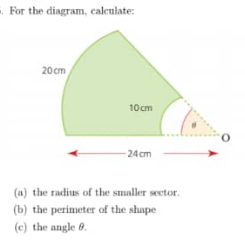
Question Number 108104 Answers: 1 Comments: 0

Question Number 108099 Answers: 3 Comments: 1
Question Number 108095 Answers: 3 Comments: 0
Pg 1102 Pg 1103 Pg 1104 Pg 1105 Pg 1106 Pg 1107 Pg 1108 Pg 1109 Pg 1110 Pg 1111
