
AllQuestion and Answers: Page 1104
Question Number 108114 Answers: 1 Comments: 0

Question Number 108107 Answers: 1 Comments: 2
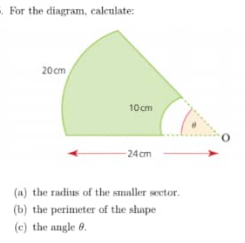
Question Number 108104 Answers: 1 Comments: 0

Question Number 108099 Answers: 3 Comments: 1
Question Number 108095 Answers: 3 Comments: 0
Question Number 108085 Answers: 2 Comments: 1
Question Number 108082 Answers: 1 Comments: 0
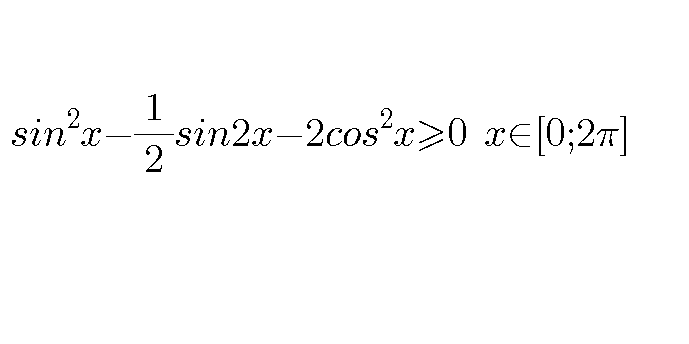
Question Number 108076 Answers: 0 Comments: 0
Question Number 108073 Answers: 3 Comments: 0
Question Number 108071 Answers: 1 Comments: 0
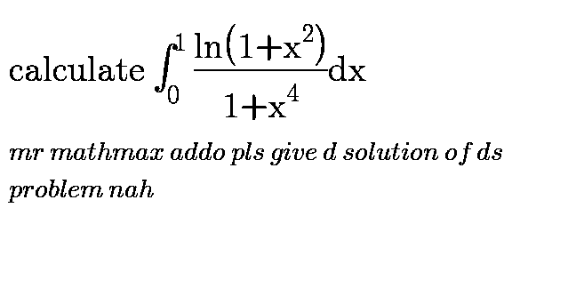
Question Number 108068 Answers: 4 Comments: 0

Question Number 108067 Answers: 2 Comments: 0

Question Number 108059 Answers: 1 Comments: 0
Question Number 108053 Answers: 2 Comments: 0
Question Number 108051 Answers: 1 Comments: 0

Question Number 108047 Answers: 1 Comments: 0
Question Number 108043 Answers: 2 Comments: 0
Question Number 108042 Answers: 0 Comments: 0
Question Number 108094 Answers: 1 Comments: 0
$$\frac{{d}^{\mathrm{2}} \Psi}{{dt}^{\mathrm{2}} }+\frac{{d}\Psi}{{dt}}+\Psi=\mathrm{0} \\ $$
Question Number 108034 Answers: 1 Comments: 0
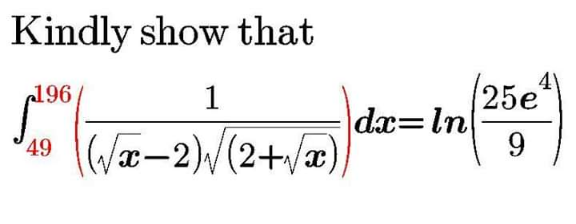
Question Number 108022 Answers: 0 Comments: 0
Question Number 108016 Answers: 1 Comments: 0

Question Number 108018 Answers: 1 Comments: 0
Question Number 108017 Answers: 2 Comments: 0
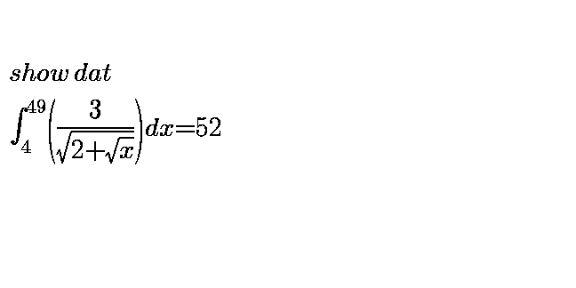
Question Number 108005 Answers: 1 Comments: 0
Question Number 107999 Answers: 3 Comments: 5

Pg 1099 Pg 1100 Pg 1101 Pg 1102 Pg 1103 Pg 1104 Pg 1105 Pg 1106 Pg 1107 Pg 1108
