
AllQuestion and Answers: Page 1094
Question Number 109642 Answers: 1 Comments: 0
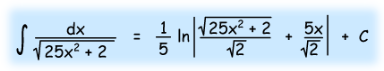
Question Number 109640 Answers: 0 Comments: 2

Question Number 109639 Answers: 2 Comments: 0

Question Number 109626 Answers: 1 Comments: 1

Question Number 109625 Answers: 0 Comments: 2
Question Number 109619 Answers: 0 Comments: 2
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}!}{{n}^{{n}} } \\ $$
Question Number 109616 Answers: 1 Comments: 1
Question Number 109611 Answers: 4 Comments: 1
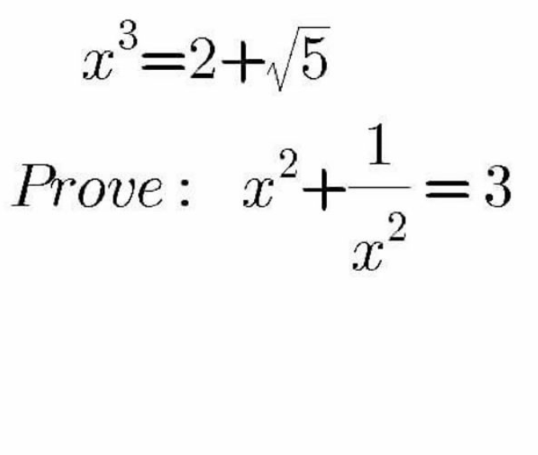
Question Number 109606 Answers: 0 Comments: 15

Question Number 109605 Answers: 0 Comments: 3

Question Number 109595 Answers: 1 Comments: 1
Question Number 109591 Answers: 1 Comments: 3
Question Number 109585 Answers: 1 Comments: 0
Question Number 109584 Answers: 3 Comments: 1
Question Number 109577 Answers: 4 Comments: 1
Question Number 109574 Answers: 0 Comments: 6
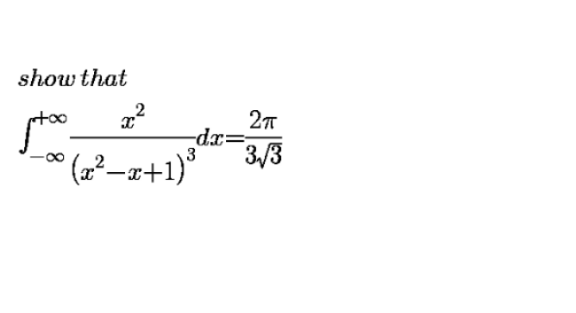
Question Number 109569 Answers: 1 Comments: 0

Question Number 109553 Answers: 1 Comments: 2
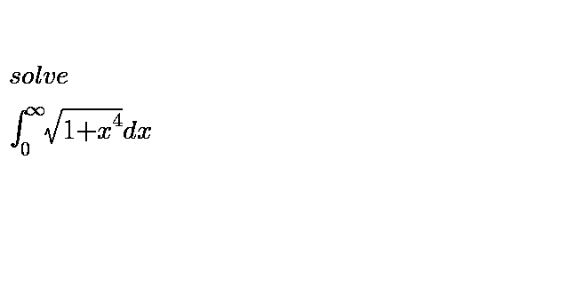
Question Number 109546 Answers: 1 Comments: 2
Question Number 109544 Answers: 2 Comments: 1
Question Number 109540 Answers: 1 Comments: 1
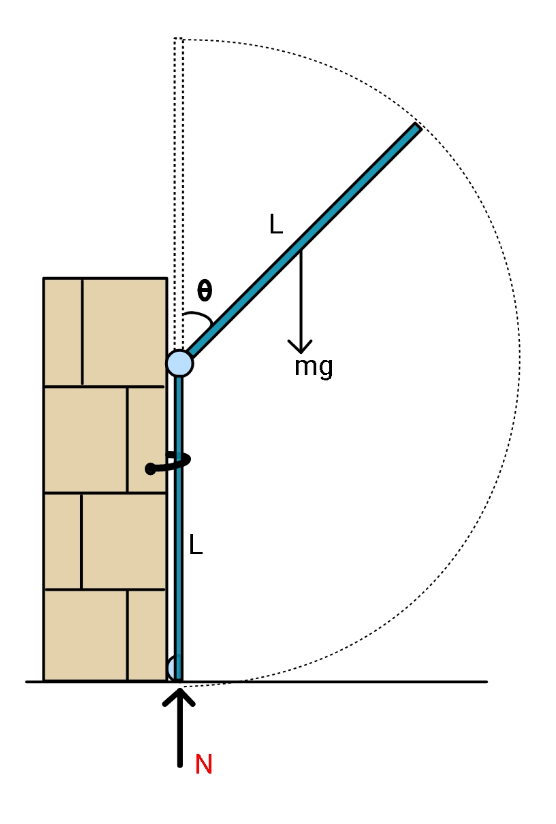
Question Number 109516 Answers: 3 Comments: 0
$$\mathrm{cos}\:\left(\mathrm{1}−{i}\right)={a}+{ib} \\ $$$${Find}\:\:{a},\:{b}. \\ $$
Question Number 109506 Answers: 0 Comments: 0

Question Number 109509 Answers: 4 Comments: 0
Question Number 109508 Answers: 2 Comments: 1

Question Number 109500 Answers: 3 Comments: 0
Pg 1089 Pg 1090 Pg 1091 Pg 1092 Pg 1093 Pg 1094 Pg 1095 Pg 1096 Pg 1097 Pg 1098
