
AllQuestion and Answers: Page 1092
Question Number 109901 Answers: 1 Comments: 0
Question Number 109895 Answers: 1 Comments: 3
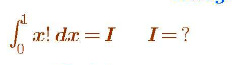
Question Number 109891 Answers: 1 Comments: 0
Question Number 109888 Answers: 3 Comments: 0
$$\mathrm{2}^{{x}+\mathrm{5}} =\sqrt{\mathrm{8}^{{x}} } \\ $$
Question Number 109884 Answers: 1 Comments: 1

Question Number 109872 Answers: 2 Comments: 1
Question Number 109863 Answers: 1 Comments: 0

Question Number 109861 Answers: 3 Comments: 0
Question Number 109858 Answers: 3 Comments: 0
Question Number 109855 Answers: 3 Comments: 0
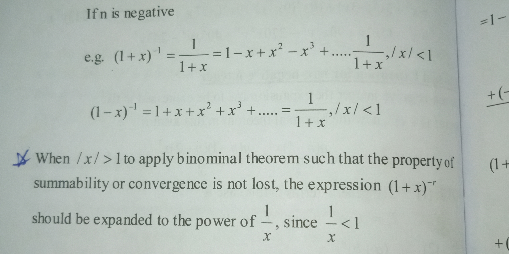
Question Number 109854 Answers: 4 Comments: 1
Question Number 109853 Answers: 0 Comments: 2
Question Number 109849 Answers: 0 Comments: 0

Question Number 109852 Answers: 0 Comments: 1
Question Number 109839 Answers: 4 Comments: 1
Question Number 109838 Answers: 1 Comments: 0
Question Number 109834 Answers: 3 Comments: 1

Question Number 109823 Answers: 1 Comments: 1

Question Number 109820 Answers: 0 Comments: 2
Question Number 109818 Answers: 1 Comments: 7
$${tanx}+{tan}\mathrm{2}{x}=\mathrm{1} \\ $$$${find}\:{the}\:{general}\:{solution} \\ $$
Question Number 109817 Answers: 0 Comments: 1

Question Number 109806 Answers: 0 Comments: 0
Question Number 109801 Answers: 0 Comments: 2
Question Number 109794 Answers: 0 Comments: 0
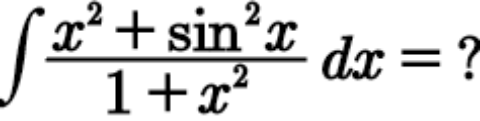
Question Number 109787 Answers: 0 Comments: 0
Question Number 109776 Answers: 0 Comments: 0
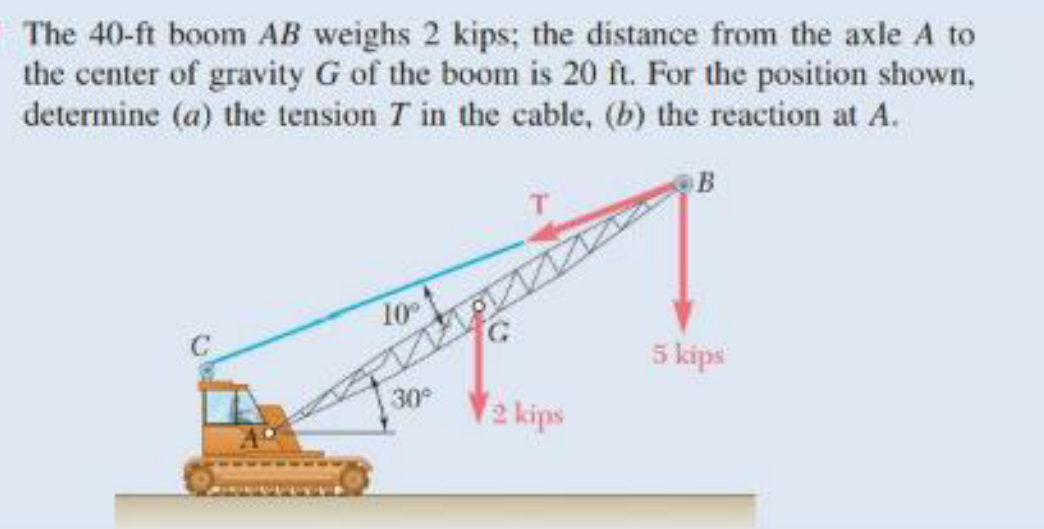
Pg 1087 Pg 1088 Pg 1089 Pg 1090 Pg 1091 Pg 1092 Pg 1093 Pg 1094 Pg 1095 Pg 1096
