
AllQuestion and Answers: Page 1084
Question Number 110875 Answers: 4 Comments: 0
Question Number 110869 Answers: 1 Comments: 0

Question Number 110868 Answers: 0 Comments: 0
Question Number 110865 Answers: 0 Comments: 0
Question Number 110861 Answers: 2 Comments: 0

Question Number 110860 Answers: 1 Comments: 0

Question Number 110858 Answers: 0 Comments: 0
Question Number 110857 Answers: 0 Comments: 0
Question Number 110856 Answers: 2 Comments: 0
$${find}\:{x}\:{in}\: \\ $$$${x}^{\mathrm{2}} =\mathrm{5}^{{x}^{\mathrm{2}} } −\mathrm{19} \\ $$
Question Number 110843 Answers: 2 Comments: 0
Question Number 110842 Answers: 0 Comments: 0

Question Number 110837 Answers: 0 Comments: 0

Question Number 110826 Answers: 0 Comments: 6
Question Number 110848 Answers: 3 Comments: 3
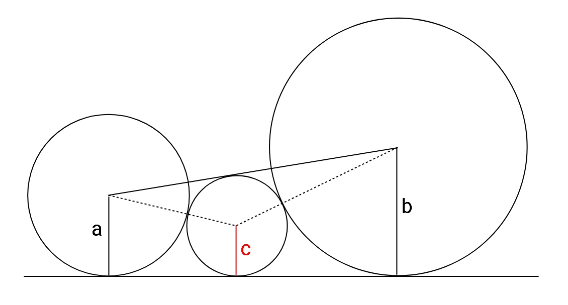
Question Number 110815 Answers: 1 Comments: 0

Question Number 110810 Answers: 1 Comments: 1
Question Number 110809 Answers: 0 Comments: 3
$${li}\underset{{x}\rightarrow\infty} {{m}}\sqrt{{x}!}=? \\ $$
Question Number 110800 Answers: 0 Comments: 0
$$\int\frac{{sin}\left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Question Number 110799 Answers: 0 Comments: 0
Question Number 110798 Answers: 0 Comments: 0
Question Number 110797 Answers: 0 Comments: 2
Question Number 110783 Answers: 0 Comments: 2
Question Number 110782 Answers: 2 Comments: 0
Question Number 110779 Answers: 1 Comments: 0
Question Number 110781 Answers: 1 Comments: 2
Question Number 111284 Answers: 0 Comments: 11
Pg 1079 Pg 1080 Pg 1081 Pg 1082 Pg 1083 Pg 1084 Pg 1085 Pg 1086 Pg 1087 Pg 1088
