
AllQuestion and Answers: Page 1083
Question Number 111011 Answers: 1 Comments: 0
Question Number 111010 Answers: 1 Comments: 0
Question Number 111008 Answers: 0 Comments: 3
Question Number 111006 Answers: 0 Comments: 2
Question Number 111002 Answers: 1 Comments: 1
Question Number 111001 Answers: 0 Comments: 1
Question Number 110993 Answers: 1 Comments: 1

Question Number 111092 Answers: 2 Comments: 4
Question Number 110988 Answers: 3 Comments: 0
Question Number 110984 Answers: 1 Comments: 3
Question Number 110980 Answers: 2 Comments: 2

Question Number 110964 Answers: 1 Comments: 0
Question Number 111017 Answers: 2 Comments: 0
Question Number 110954 Answers: 1 Comments: 0
Question Number 110953 Answers: 0 Comments: 1

Question Number 110951 Answers: 2 Comments: 0
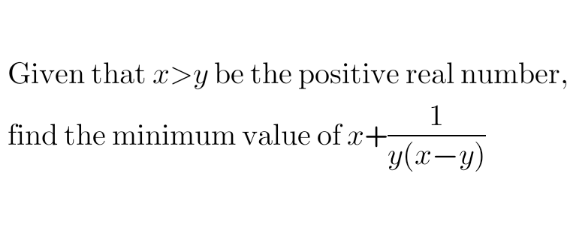
Question Number 110948 Answers: 1 Comments: 6
Question Number 110944 Answers: 5 Comments: 3
Question Number 110939 Answers: 2 Comments: 1
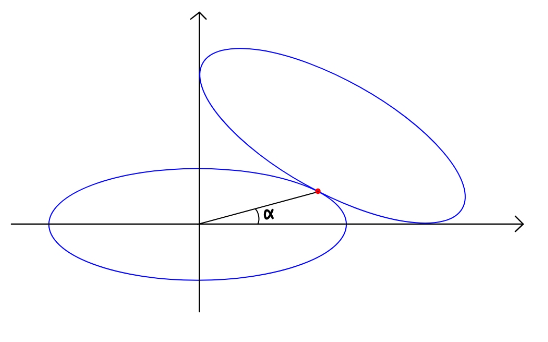
Question Number 110926 Answers: 1 Comments: 0
Question Number 110970 Answers: 2 Comments: 1

Question Number 110911 Answers: 0 Comments: 0
Question Number 110910 Answers: 2 Comments: 0
Question Number 110897 Answers: 3 Comments: 0
Question Number 110895 Answers: 3 Comments: 0
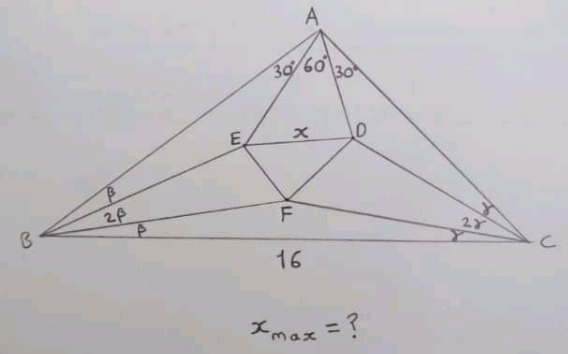
Question Number 110879 Answers: 0 Comments: 1
Pg 1078 Pg 1079 Pg 1080 Pg 1081 Pg 1082 Pg 1083 Pg 1084 Pg 1085 Pg 1086 Pg 1087
