
AllQuestion and Answers: Page 1082
Question Number 110616 Answers: 1 Comments: 0
Question Number 110614 Answers: 1 Comments: 0

Question Number 110608 Answers: 0 Comments: 1
Question Number 110704 Answers: 3 Comments: 0
Question Number 110596 Answers: 1 Comments: 2
Question Number 110595 Answers: 0 Comments: 5
$$\mathrm{Evaluate}\:\mathrm{5}!\bullet\mathrm{6}!\left(\mathrm{mod}\:\mathrm{7}!\right) \\ $$
Question Number 110594 Answers: 1 Comments: 0
Question Number 110593 Answers: 1 Comments: 0
Question Number 110592 Answers: 3 Comments: 0
Question Number 110591 Answers: 3 Comments: 0
Question Number 110673 Answers: 2 Comments: 0
Question Number 110587 Answers: 1 Comments: 0
Question Number 110586 Answers: 1 Comments: 0
Question Number 110725 Answers: 2 Comments: 0
$${x}^{{x}^{{x}^{{x}^{...} } } } =\mathrm{2}\:\:\:\:\:\:\:{x}=? \\ $$
Question Number 110562 Answers: 2 Comments: 0
Question Number 110565 Answers: 0 Comments: 15
Question Number 110688 Answers: 0 Comments: 0
Question Number 110551 Answers: 2 Comments: 0
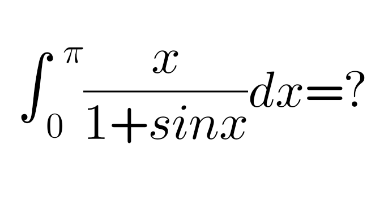
Question Number 110550 Answers: 0 Comments: 0

Question Number 110549 Answers: 2 Comments: 1
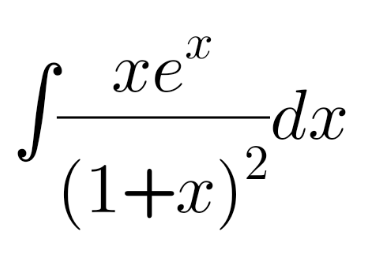
Question Number 110545 Answers: 1 Comments: 2
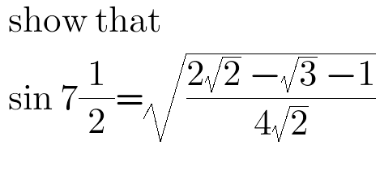
Question Number 110543 Answers: 1 Comments: 0

Question Number 113557 Answers: 1 Comments: 0
Question Number 113644 Answers: 1 Comments: 0

Question Number 110539 Answers: 0 Comments: 4
Question Number 110644 Answers: 1 Comments: 1
Pg 1077 Pg 1078 Pg 1079 Pg 1080 Pg 1081 Pg 1082 Pg 1083 Pg 1084 Pg 1085 Pg 1086
