
AllQuestion and Answers: Page 1081
Question Number 111189 Answers: 4 Comments: 0
Question Number 111187 Answers: 1 Comments: 1
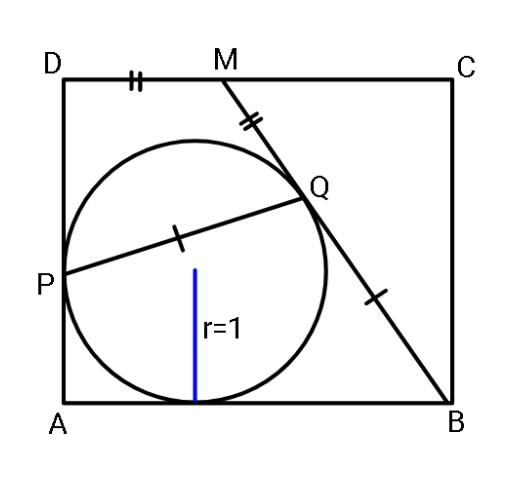
Question Number 111183 Answers: 2 Comments: 1
Question Number 111180 Answers: 0 Comments: 0
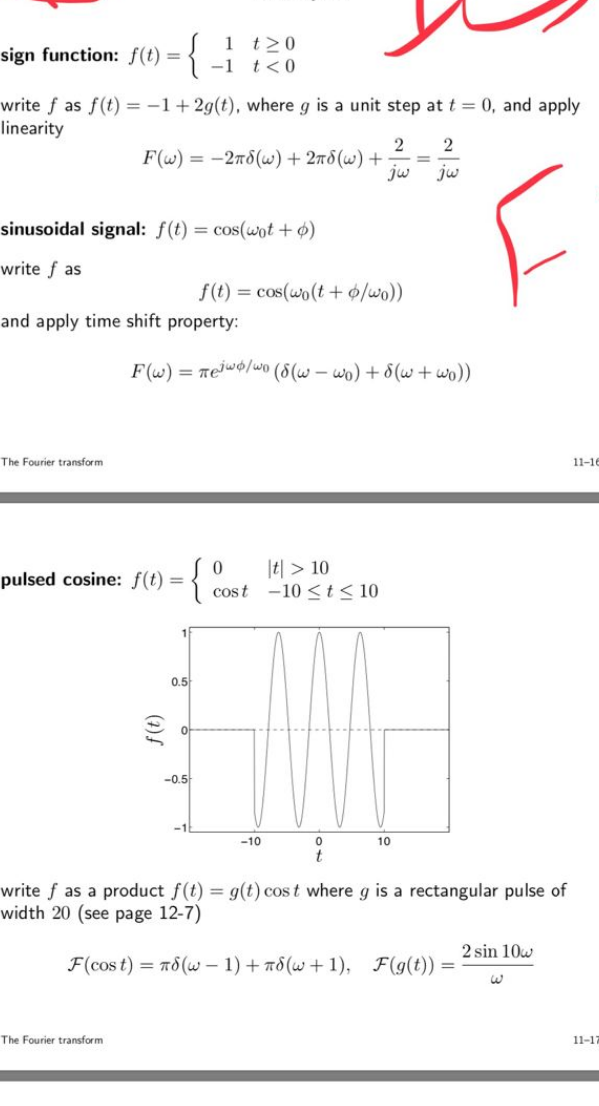
$${solve}:\:{x}^{\mathrm{2}} {y}\left({ydx}+{dy}\right)=\mathrm{2}{ydx}+{xdy} \\ $$
Question Number 111272 Answers: 1 Comments: 0
Question Number 111175 Answers: 1 Comments: 0
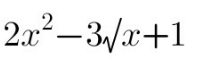
Question Number 111174 Answers: 0 Comments: 0
Question Number 112273 Answers: 1 Comments: 2
Question Number 111275 Answers: 1 Comments: 0
Question Number 111163 Answers: 1 Comments: 2
Question Number 111159 Answers: 2 Comments: 0
Question Number 111157 Answers: 2 Comments: 0
Question Number 111155 Answers: 1 Comments: 0
Question Number 111154 Answers: 0 Comments: 2
Question Number 111276 Answers: 1 Comments: 0
Question Number 111149 Answers: 0 Comments: 4
Question Number 111279 Answers: 1 Comments: 0
Question Number 111147 Answers: 0 Comments: 0

Question Number 111477 Answers: 1 Comments: 0
Question Number 111140 Answers: 0 Comments: 0
Question Number 111135 Answers: 2 Comments: 0

Question Number 111134 Answers: 0 Comments: 0
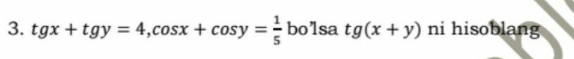
Question Number 111132 Answers: 1 Comments: 0
Question Number 111125 Answers: 1 Comments: 0
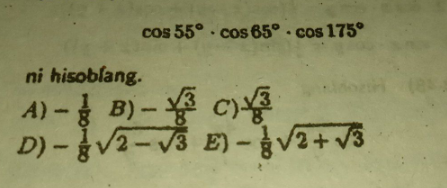
Question Number 111152 Answers: 0 Comments: 0
Question Number 111282 Answers: 1 Comments: 0
Pg 1076 Pg 1077 Pg 1078 Pg 1079 Pg 1080 Pg 1081 Pg 1082 Pg 1083 Pg 1084 Pg 1085
