
AllQuestion and Answers: Page 1080
Question Number 111357 Answers: 0 Comments: 0
Question Number 111351 Answers: 2 Comments: 0
Question Number 111347 Answers: 0 Comments: 0
Question Number 111344 Answers: 0 Comments: 3
Question Number 111343 Answers: 0 Comments: 1
Question Number 111342 Answers: 1 Comments: 0
Question Number 111340 Answers: 1 Comments: 2
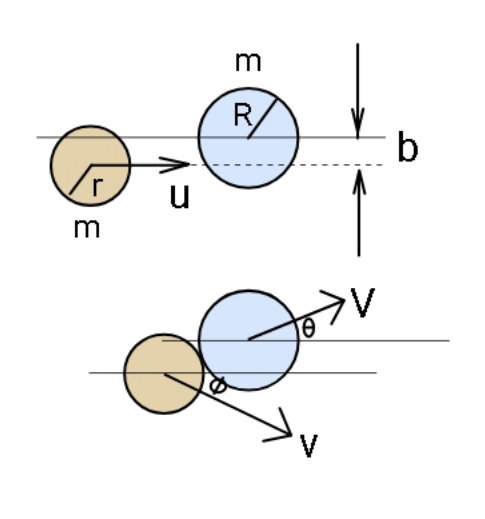
Question Number 111330 Answers: 0 Comments: 0
Question Number 111326 Answers: 2 Comments: 0
Question Number 111313 Answers: 4 Comments: 0
Question Number 111277 Answers: 1 Comments: 0
Question Number 111267 Answers: 1 Comments: 0
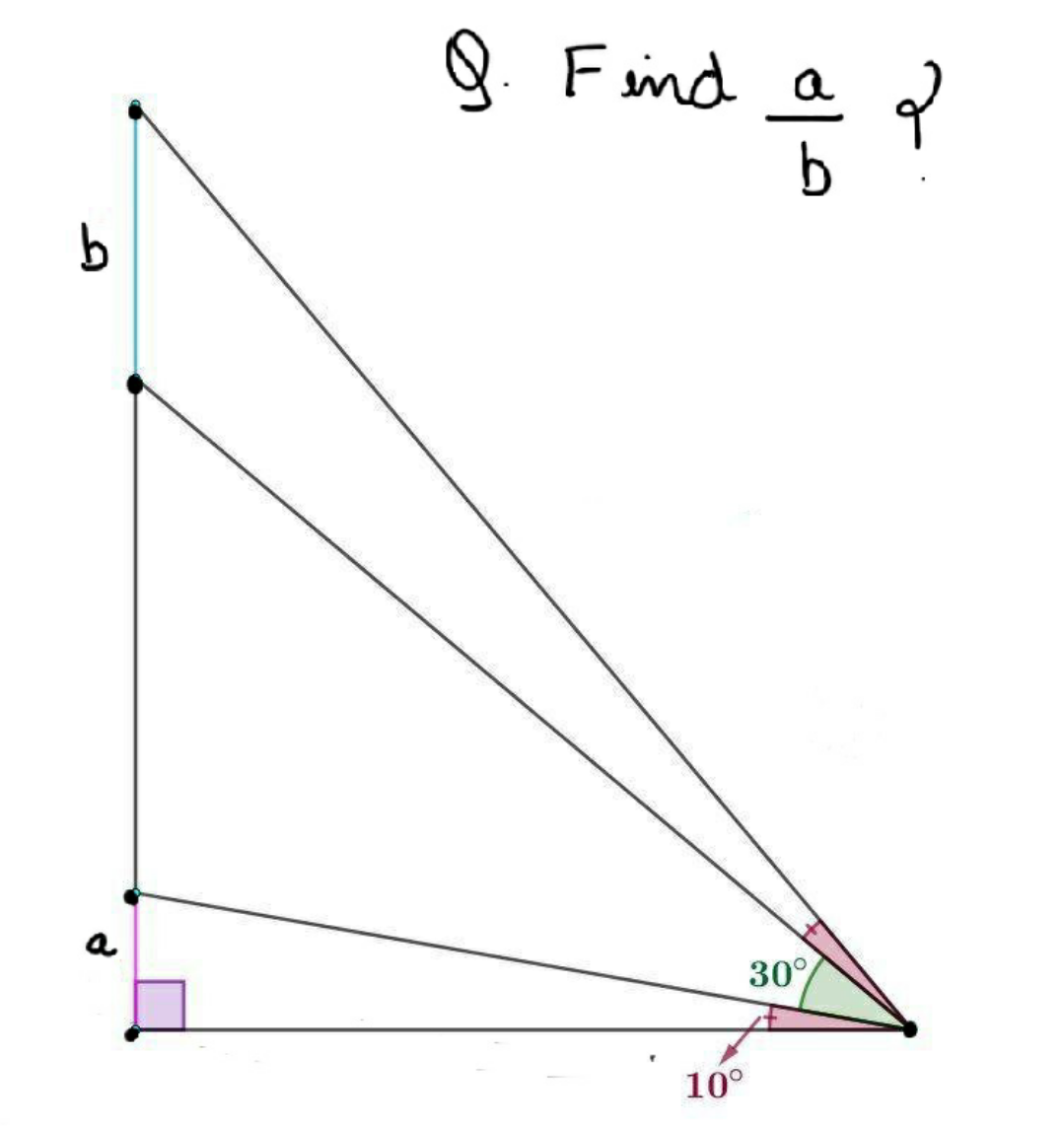
Question Number 111264 Answers: 1 Comments: 1

Question Number 111259 Answers: 1 Comments: 1
Question Number 111218 Answers: 1 Comments: 0
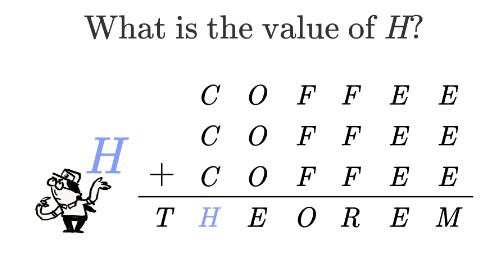
Question Number 111216 Answers: 3 Comments: 2

Question Number 111213 Answers: 2 Comments: 0
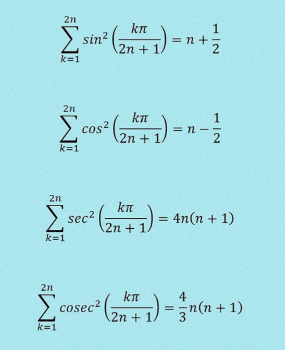
Question Number 111209 Answers: 0 Comments: 6
Question Number 111208 Answers: 1 Comments: 3
Question Number 111235 Answers: 1 Comments: 1
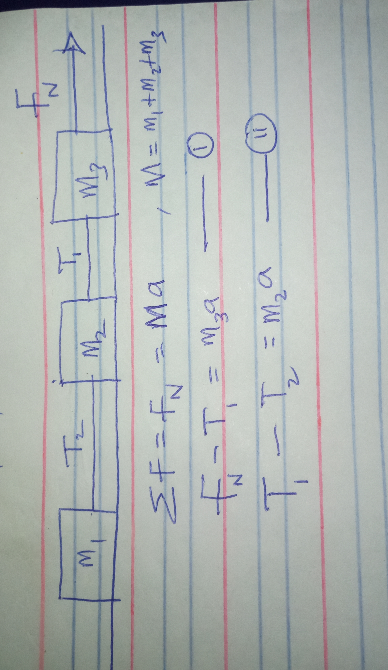
Question Number 111206 Answers: 1 Comments: 0
$$\int\:\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{5}} \\ $$
Question Number 111205 Answers: 0 Comments: 1
Question Number 112193 Answers: 0 Comments: 1

Question Number 111196 Answers: 1 Comments: 0
Question Number 111195 Answers: 2 Comments: 0
Question Number 111189 Answers: 4 Comments: 0
Pg 1075 Pg 1076 Pg 1077 Pg 1078 Pg 1079 Pg 1080 Pg 1081 Pg 1082 Pg 1083 Pg 1084
