
AllQuestion and Answers: Page 1072
Question Number 111869 Answers: 0 Comments: 0
Question Number 111868 Answers: 2 Comments: 0
Question Number 111859 Answers: 2 Comments: 7
Question Number 111850 Answers: 4 Comments: 0
Question Number 112531 Answers: 0 Comments: 4
Question Number 111831 Answers: 1 Comments: 0
Question Number 112535 Answers: 1 Comments: 5
Question Number 111818 Answers: 3 Comments: 0
Question Number 111813 Answers: 0 Comments: 3
Question Number 111799 Answers: 3 Comments: 4
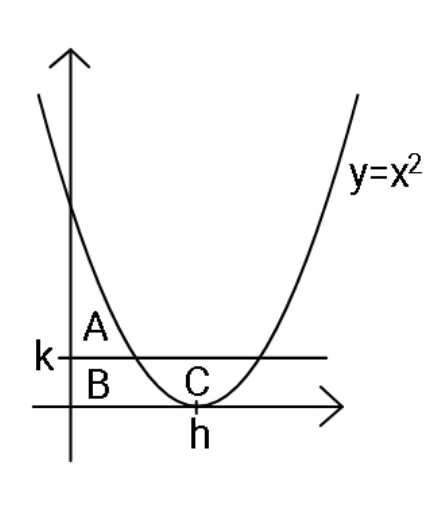
Question Number 111788 Answers: 1 Comments: 0

Question Number 111781 Answers: 0 Comments: 3
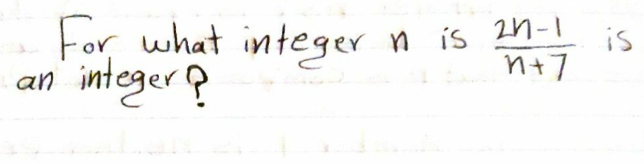
Question Number 111774 Answers: 1 Comments: 0

Question Number 111772 Answers: 1 Comments: 0
Question Number 111771 Answers: 0 Comments: 0
Question Number 111770 Answers: 0 Comments: 0
Question Number 111769 Answers: 0 Comments: 0
Question Number 111768 Answers: 0 Comments: 0
Question Number 111766 Answers: 2 Comments: 0
Question Number 111762 Answers: 1 Comments: 0
Question Number 111760 Answers: 0 Comments: 0
Question Number 111756 Answers: 0 Comments: 0
Question Number 111755 Answers: 2 Comments: 0
Question Number 111754 Answers: 2 Comments: 0
Question Number 111887 Answers: 0 Comments: 0
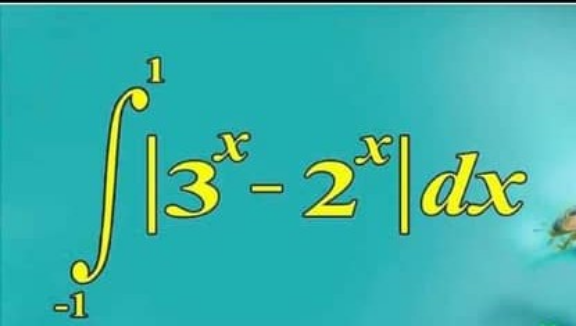
Question Number 111882 Answers: 1 Comments: 0
Pg 1067 Pg 1068 Pg 1069 Pg 1070 Pg 1071 Pg 1072 Pg 1073 Pg 1074 Pg 1075 Pg 1076
