Question and Answers Forum

AllQuestion and Answers: Page 1067

Question Number 113006 Answers: 1 Comments: 0

a+(1/(b+(1/(c+(1/(d+...))))))=(2)^(1/3) If a,b,c,d,... are positive integers, then what is the value of ′b′?

$$\mathrm{a}+\frac{\mathrm{1}}{\mathrm{b}+\frac{\mathrm{1}}{\mathrm{c}+\frac{\mathrm{1}}{\mathrm{d}+...}}}=\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$$\mathrm{If}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},...\:\mathrm{are}\:\mathrm{positive}\:\mathrm{integers},\:\mathrm{then} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:'\mathrm{b}'? \\ $$

Question Number 113005 Answers: 1 Comments: 0

Two different two−digit natural numbers are written beside each other such that the larger number is written on the left. When the absolute difference of the two numbers is subtracted from the four−digit number so formed, the number obtained is 5481. What is the sum of the two−digit numbers?

$$\mathrm{Two}\:\mathrm{different}\:\mathrm{two}−\mathrm{digit}\:\mathrm{natural} \\ $$$$\mathrm{numbers}\:\mathrm{are}\:\mathrm{written}\:\mathrm{beside}\:\mathrm{each} \\ $$$$\mathrm{other}\:\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{larger}\:\mathrm{number} \\ $$$$\mathrm{is}\:\mathrm{written}\:\mathrm{on}\:\mathrm{the}\:\mathrm{left}.\:\mathrm{When}\:\mathrm{the} \\ $$$$\mathrm{absolute}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two} \\ $$$$\mathrm{numbers}\:\mathrm{is}\:\mathrm{subtracted}\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{four}−\mathrm{digit}\:\mathrm{number}\:\mathrm{so}\:\mathrm{formed},\:\mathrm{the} \\ $$$$\mathrm{number}\:\mathrm{obtained}\:\mathrm{is}\:\mathrm{5481}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two}−\mathrm{digit}\:\mathrm{numbers}? \\ $$

Question Number 113004 Answers: 2 Comments: 0

prove that _0 ∫^( ∞) cos(x^2 )dx = _0 ∫^( ∞) sin(x^2 )dx =((√π)/(2(√2)))

$${prove}\:{that} \\ $$$$\:_{\mathrm{0}} \int^{\:\infty} \:{cos}\left({x}^{\mathrm{2}} \right){dx}\:=\:\:_{\mathrm{0}} \int^{\:\infty} {sin}\left({x}^{\mathrm{2}} \right){dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$

Question Number 113003 Answers: 1 Comments: 2

The digits of a three−digit number A are written in the reverse order to form another three−digit number B. If B>A and B−A is perfectly divisible by 7. Find the range of values of A.

$$\mathrm{The}\:\mathrm{digits}\:\mathrm{of}\:\mathrm{a}\:\mathrm{three}−\mathrm{digit}\:\mathrm{number}\:\mathrm{A} \\ $$$$\mathrm{are}\:\mathrm{written}\:\mathrm{in}\:\mathrm{the}\:\mathrm{reverse}\:\mathrm{order}\:\mathrm{to} \\ $$$$\mathrm{form}\:\mathrm{another}\:\mathrm{three}−\mathrm{digit}\:\mathrm{number}\:\mathrm{B}. \\ $$$$\mathrm{If}\:\mathrm{B}>\mathrm{A}\:\mathrm{and}\:\mathrm{B}−\mathrm{A}\:\mathrm{is}\:\mathrm{perfectly} \\ $$$$\mathrm{divisible}\:\mathrm{by}\:\mathrm{7}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of} \\ $$$$\mathrm{values}\:\mathrm{of}\:\mathrm{A}. \\ $$

Question Number 113002 Answers: 1 Comments: 0

After distributing sweets equally among 25 children, 8 sweets remained. Had the number of children been 28, 22 sweets would have been left after equally distributing. What was the total number of sweets?

$$\mathrm{After}\:\mathrm{distributing}\:\mathrm{sweets}\:\mathrm{equally} \\ $$$$\mathrm{among}\:\mathrm{25}\:\mathrm{children},\:\mathrm{8}\:\mathrm{sweets} \\ $$$$\mathrm{remained}.\:\mathrm{Had}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{children} \\ $$$$\mathrm{been}\:\mathrm{28},\:\mathrm{22}\:\mathrm{sweets}\:\mathrm{would}\:\mathrm{have}\:\mathrm{been} \\ $$$$\mathrm{left}\:\mathrm{after}\:\mathrm{equally}\:\mathrm{distributing}.\:\mathrm{What} \\ $$$$\mathrm{was}\:\mathrm{the}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{sweets}? \\ $$

Question Number 113001 Answers: 0 Comments: 1

N! is completely divisible by 13^(52) . What is the sum of the digits of the smallest such number N?

$$\mathrm{N}!\:\mathrm{is}\:\mathrm{completely}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{13}^{\mathrm{52}} . \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{smallest}\:\mathrm{such}\:\mathrm{number}\:\mathrm{N}? \\ $$

Question Number 113000 Answers: 1 Comments: 0

The first 23 natural numbers are written in an increasing order beside each other to form a single number. What is the remainder when this number is divided by 18?

$$\mathrm{The}\:\mathrm{first}\:\mathrm{23}\:\mathrm{natural}\:\mathrm{numbers} \\ $$$$\mathrm{are}\:\mathrm{written}\:\mathrm{in}\:\mathrm{an}\:\mathrm{increasing}\:\mathrm{order} \\ $$$$\mathrm{beside}\:\mathrm{each}\:\mathrm{other}\:\mathrm{to}\:\mathrm{form}\:\mathrm{a}\:\mathrm{single} \\ $$$$\mathrm{number}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when} \\ $$$$\mathrm{this}\:\mathrm{number}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{18}? \\ $$

Question Number 112999 Answers: 1 Comments: 0

Product of divisors of 7056 ?

$$\mathrm{Product}\:\mathrm{of}\:\mathrm{divisors}\:\mathrm{of}\:\mathrm{7056}\:? \\ $$

Question Number 112998 Answers: 1 Comments: 0

If x+y+z=1 and x,y,z are positive real numbers, then the least value of ((1/x)−1)((1/y)−1)((1/z)−1) is

$$\mathrm{If}\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1}\:\mathrm{and}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{are}\:\mathrm{positive} \\ $$$$\mathrm{real}\:\mathrm{numbers},\:\mathrm{then}\:\mathrm{the}\:\mathrm{least}\:\mathrm{value}\:\mathrm{of} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{y}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{z}}−\mathrm{1}\right)\:\mathrm{is}\: \\ $$

Question Number 112997 Answers: 1 Comments: 3

∫(( tan x dx)/( (√(sec^3 x + 1)))) = ?

$$\int\frac{\:{tan}\:{x}\:{dx}}{\:\sqrt{{sec}^{\mathrm{3}} \:{x}\:+\:\mathrm{1}}}\:=\:? \\ $$

Question Number 112996 Answers: 1 Comments: 0

Find the last digit of the sum 19^(81) +4^(9k) , k∈N

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{19}^{\mathrm{81}} +\mathrm{4}^{\mathrm{9k}} ,\:\mathrm{k}\in\mathrm{N} \\ $$

Question Number 112992 Answers: 1 Comments: 1

Question Number 112986 Answers: 0 Comments: 0

Question Number 112974 Answers: 2 Comments: 0

solve lim_(x→∞) (((2x^3 −x^2 +2)/(2x^3 −4x^2 +1)))^x

$$\mathrm{solve}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{x}} \\ $$

Question Number 112971 Answers: 1 Comments: 1

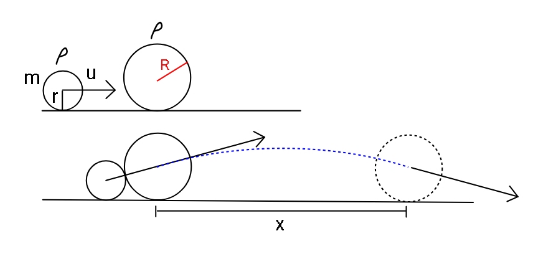
Question Number 112962 Answers: 4 Comments: 3

Question Number 112994 Answers: 1 Comments: 0

If n is any even number, then n(n^2 +20) is always divisible by?

$$\mathrm{If}\:\mathrm{n}\:\mathrm{is}\:\mathrm{any}\:\mathrm{even}\:\mathrm{number},\:\mathrm{then} \\ $$$$\mathrm{n}\left(\mathrm{n}^{\mathrm{2}} +\mathrm{20}\right)\:\mathrm{is}\:\mathrm{always}\:\mathrm{divisible}\:\mathrm{by}? \\ $$

Question Number 112958 Answers: 0 Comments: 3

Question Number 112934 Answers: 1 Comments: 7

There are 4 identical mathematics books, 2 identical physics books, 2 identical chemistry books and 2 identical biology books. in how many ways can you compile the 10 books such that same books are not mutually adjacent.

$$\mathrm{There}\:\mathrm{are}\:\mathrm{4}\:\mathrm{identical}\:\mathrm{mathematics} \\ $$$$\mathrm{books},\:\mathrm{2}\:\mathrm{identical}\:\mathrm{physics}\:\mathrm{books},\:\mathrm{2} \\ $$$$\mathrm{identical}\:\mathrm{chemistry}\:\mathrm{books}\:\mathrm{and}\:\mathrm{2} \\ $$$$\mathrm{identical}\:\mathrm{biology}\:\mathrm{books}.\:\mathrm{in}\:\mathrm{how}\:\mathrm{many} \\ $$$$\mathrm{ways}\:\:\mathrm{can}\:\mathrm{you}\:\mathrm{compile}\:\mathrm{the}\:\mathrm{10}\:\mathrm{books} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{same}\:\mathrm{books}\:\mathrm{are}\:\mathrm{not}\:\mathrm{mutually} \\ $$$$\mathrm{adjacent}. \\ $$

Question Number 112917 Answers: 1 Comments: 3

lim_(x→∞) [csc^2 ((2/x))−(1/4)x^2 ]

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\mathrm{csc}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} \right] \\ $$

Question Number 112908 Answers: 2 Comments: 1

if the angle between( kx+5y=1 , kx−2y=2)equal 60^° then k=? help me sir

$${if}\:{the}\:{angle}\:{between}\left(\:{kx}+\mathrm{5}{y}=\mathrm{1}\:,\:{kx}−\mathrm{2}{y}=\mathrm{2}\right){equal}\:\mathrm{60}^{°} {then}\:{k}=? \\ $$$$ \\ $$$${help}\:{me}\:{sir} \\ $$

Question Number 112906 Answers: 0 Comments: 4

prove that (B^(−1) )(A^(−1) )=(AB)^(−1) if A=(34,12),B=(12,−13) please sir help me

$${prove}\:{that}\:\left({B}^{−\mathrm{1}} \right)\left({A}^{−\mathrm{1}} \right)=\left({AB}\right)^{−\mathrm{1}} \:{if}\:{A}=\left(\mathrm{34},\mathrm{12}\right),{B}=\left(\mathrm{12},−\mathrm{13}\right) \\ $$$${please}\:{sir}\:{help}\:{me} \\ $$

Question Number 112904 Answers: 1 Comments: 0

solve the equation y+x=3, 2y+x=5 by ussing matrixis method help me sir please ?