
AllQuestion and Answers: Page 1061
Question Number 113375 Answers: 0 Comments: 1
Question Number 113374 Answers: 1 Comments: 5
Question Number 113372 Answers: 1 Comments: 2
Question Number 113278 Answers: 2 Comments: 0
Question Number 113275 Answers: 2 Comments: 0
Question Number 113274 Answers: 4 Comments: 2
Question Number 113272 Answers: 2 Comments: 0
Question Number 113271 Answers: 0 Comments: 0
Question Number 113262 Answers: 2 Comments: 0
Question Number 113261 Answers: 1 Comments: 0
Question Number 113246 Answers: 1 Comments: 1

Question Number 113243 Answers: 1 Comments: 3
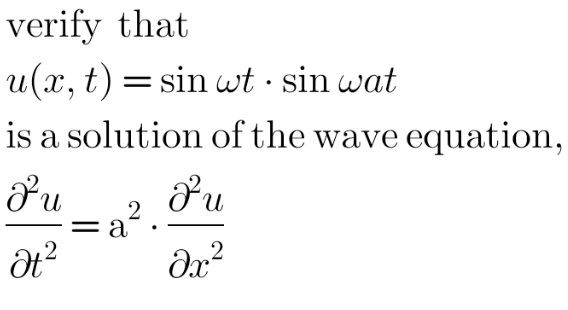
Question Number 113241 Answers: 1 Comments: 0

Question Number 113237 Answers: 1 Comments: 0
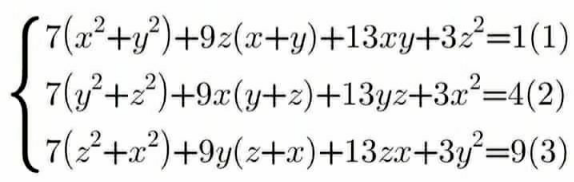
Question Number 121155 Answers: 0 Comments: 0

Question Number 113221 Answers: 0 Comments: 3
Question Number 113219 Answers: 1 Comments: 0
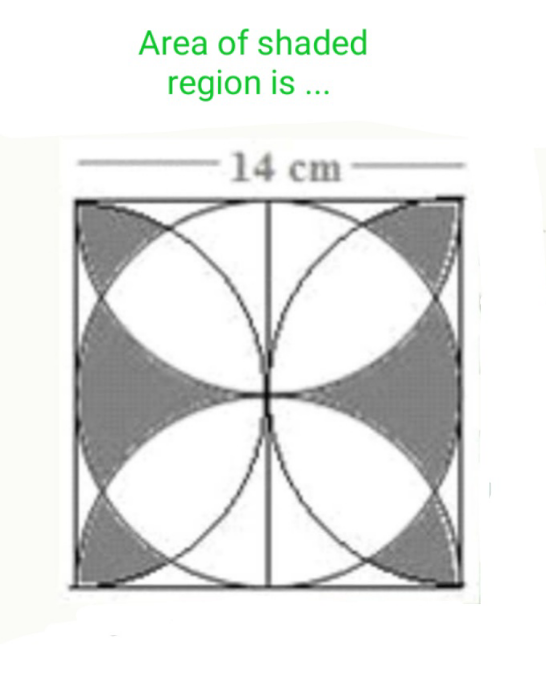
Question Number 113218 Answers: 1 Comments: 0

Question Number 113211 Answers: 3 Comments: 0
Question Number 113203 Answers: 1 Comments: 0
Question Number 113200 Answers: 2 Comments: 0
Question Number 113199 Answers: 1 Comments: 8
Question Number 113198 Answers: 1 Comments: 0
Question Number 113196 Answers: 1 Comments: 0
Question Number 113191 Answers: 1 Comments: 0
Question Number 113190 Answers: 1 Comments: 3
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}−\mathrm{1}}{dx} \\ $$
Pg 1056 Pg 1057 Pg 1058 Pg 1059 Pg 1060 Pg 1061 Pg 1062 Pg 1063 Pg 1064 Pg 1065
