
AllQuestion and Answers: Page 1051
Question Number 114981 Answers: 2 Comments: 2
Question Number 114980 Answers: 1 Comments: 0

Question Number 114978 Answers: 2 Comments: 0
Question Number 114975 Answers: 1 Comments: 0
Question Number 114967 Answers: 0 Comments: 1

Question Number 114965 Answers: 1 Comments: 0
Question Number 114996 Answers: 2 Comments: 1
Question Number 114959 Answers: 2 Comments: 0
Question Number 114956 Answers: 0 Comments: 5

Question Number 114950 Answers: 0 Comments: 0
Question Number 114945 Answers: 1 Comments: 0

Question Number 114943 Answers: 1 Comments: 0
Question Number 114971 Answers: 0 Comments: 2

Question Number 114933 Answers: 2 Comments: 0
Question Number 114922 Answers: 2 Comments: 0
Question Number 114919 Answers: 0 Comments: 0

Question Number 114912 Answers: 0 Comments: 0

Question Number 114917 Answers: 0 Comments: 3

Question Number 114906 Answers: 3 Comments: 1
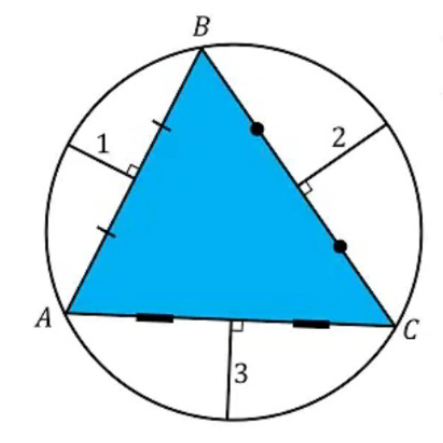
Question Number 114880 Answers: 1 Comments: 1
$$\int\mathrm{ln}\:\left(\mathrm{sin}\:\left({x}\right)\right){dx}=? \\ $$
Question Number 114879 Answers: 1 Comments: 0
Question Number 114878 Answers: 2 Comments: 0
Question Number 114876 Answers: 2 Comments: 1

Question Number 114875 Answers: 2 Comments: 0
Question Number 114863 Answers: 1 Comments: 0
Question Number 114860 Answers: 0 Comments: 3

Pg 1046 Pg 1047 Pg 1048 Pg 1049 Pg 1050 Pg 1051 Pg 1052 Pg 1053 Pg 1054 Pg 1055
