Question and Answers Forum

AllQuestion and Answers: Page 1048

Question Number 113789 Answers: 2 Comments: 0

Σ_(n=1) ^∝ (3/(n(n+3)))=?

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\propto} {\sum}}\frac{\mathrm{3}}{\mathrm{n}\left(\mathrm{n}+\mathrm{3}\right)}=? \\ $$

Question Number 113786 Answers: 2 Comments: 0

Question Number 113781 Answers: 4 Comments: 0

Question Number 113771 Answers: 1 Comments: 0

Question Number 113770 Answers: 0 Comments: 0

Question Number 113769 Answers: 2 Comments: 0

prove that, tan (7(1/2))°=(√6)−(√3)+(√2)−2

$${prove}\:{that},\:\mathrm{tan}\:\left(\mathrm{7}\frac{\mathrm{1}}{\mathrm{2}}\right)°=\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}−\mathrm{2} \\ $$

Question Number 113775 Answers: 0 Comments: 1

Question Number 113767 Answers: 0 Comments: 1

$$ \\ $$$$ \\ $$

Question Number 113766 Answers: 1 Comments: 0

I=∫_0 ^∞ ((π/(1+π^2 x^2 ))−(1/(1+x^2 )))lnx dx put πx=tanA, x =tanB I=∫_0 ^(π/2) (ln(tanA)−lnπ)dA−∫_0 ^(π/2) ln(tanB)dB I=((−π)/2)lnπ

$$ \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \left(\frac{\pi}{\mathrm{1}+\pi^{\mathrm{2}} {x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){lnx}\:{dx} \\ $$$${put}\:\pi{x}={tanA},\:{x}\:={tanB} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left({ln}\left({tanA}\right)−{ln}\pi\right){dA}−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {ln}\left({tanB}\right){dB} \\ $$$${I}=\frac{−\pi}{\mathrm{2}}{ln}\pi \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 113763 Answers: 0 Comments: 0

Question Number 113760 Answers: 1 Comments: 0

∫(√((x−1)/x^5 ))dx

$$\int\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }}\mathrm{dx} \\ $$

Question Number 113747 Answers: 3 Comments: 0

lim_(x→0) ((sin^(−1) x)/x)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{−\mathrm{1}} {x}}{{x}} \\ $$

Question Number 113745 Answers: 1 Comments: 0

Question Number 113740 Answers: 1 Comments: 0

In triangle ABC has positive integer sides ; ∠A = 2 ∠B and ∠C > (π/2). What is the minimum length of the perimeter of the triangle?

$${In}\:{triangle}\:{ABC}\:{has}\:{positive}\:{integer} \\ $$$${sides}\:;\:\angle{A}\:=\:\mathrm{2}\:\angle{B}\:{and}\:\angle{C}\:>\:\frac{\pi}{\mathrm{2}}. \\ $$$${What}\:{is}\:{the}\:{minimum}\:{length} \\ $$$${of}\:{the}\:{perimeter}\:{of}\:{the}\:{triangle}?\: \\ $$

Question Number 113738 Answers: 1 Comments: 0

∫_0 ^π ((x sin x)/(1+cos^2 x)) dx ?

$$\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{x}\:\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:? \\ $$

Question Number 113714 Answers: 1 Comments: 0

Question Number 113710 Answers: 1 Comments: 2

you have 2 identical mathematics books, 2 identical physics books, 2 identical chemistry books, 2 identical biology books and 2 geography books. in how many ways can you compile these books such that same books are not mutually adjacent?

$${you}\:{have}\:\mathrm{2}\:{identical}\:{mathematics} \\ $$$${books},\:\mathrm{2}\:{identical}\:{physics}\:{books},\:\mathrm{2} \\ $$$${identical}\:{chemistry}\:{books},\:\mathrm{2}\:{identical} \\ $$$${biology}\:{books}\:{and}\:\mathrm{2}\:{geography}\:{books}. \\ $$$${in}\:{how}\:{many}\:{ways}\:{can}\:{you}\:{compile} \\ $$$${these}\:{books}\:{such}\:{that}\:{same}\:{books} \\ $$$${are}\:{not}\:{mutually}\:{adjacent}? \\ $$

Question Number 113706 Answers: 4 Comments: 0

∫(√(tanx)) dx =?

$$\:\:\:\int\sqrt{\mathrm{tanx}}\:\mathrm{dx}\:=?\:\:\:\: \\ $$

Question Number 113757 Answers: 2 Comments: 0

∫ (dx/(tan x−sin x)) ?

$$\:\int\:\frac{{dx}}{\mathrm{tan}\:{x}−\mathrm{sin}\:{x}}\:?\: \\ $$

Question Number 113756 Answers: 2 Comments: 1

∫_0 ^1 ((log(x+1))/x)dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}+\mathrm{1}\right)}{{x}}{dx} \\ $$

Question Number 113708 Answers: 1 Comments: 1

∫x^x dx =?

$$\:\:\:\:\:\int\mathrm{x}^{\mathrm{x}} \:\mathrm{dx}\:=?\:\: \\ $$

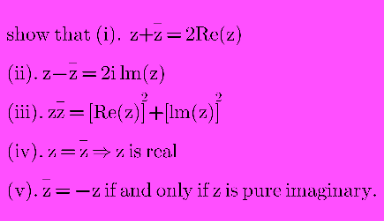
Question Number 113689 Answers: 3 Comments: 1

Find p and q such that p^2 +q^2 =101^2 . Where p, q∈Z different from zero.

$$\mathrm{Find}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{101}^{\mathrm{2}} .\:\mathrm{Where}\:\mathrm{p},\:\mathrm{q}\in\mathbb{Z}\: \\ $$$$\mathrm{different}\:\mathrm{from}\:\mathrm{zero}. \\ $$

Question Number 114192 Answers: 1 Comments: 0

For a positive integer k, we write (1+x)(1+2x)(1+3x)...(1+kx)=a_0 +a_1 x+a_2 x^2 +...a_k x^k Let N=a_0 +a_1 +a_2 +...a_k , if N is divisible by 2019, find the smallest possible value of k.

$$\mathrm{For}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{integer}\:{k},\:\mathrm{we}\:\mathrm{write}\: \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{1}+\mathrm{3}{x}\right)...\left(\mathrm{1}+{kx}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +...{a}_{{k}} {x}^{{k}} \\ $$$$\mathrm{Let}\:{N}={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...{a}_{{k}} \:, \\ $$$$\mathrm{if}\:{N}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2019},\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{smallest}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:{k}. \\ $$

Question Number 113684 Answers: 1 Comments: 1

A nice question <3 If a quadratic equation (1−q+(p^2 /2))x^2 +p(1+q)x+q(q−1)+(p^2 /2)=0 has equal roots, prove that p^2 =4q

$$\mathrm{A}\:\mathrm{nice}\:\mathrm{question}\:<\mathrm{3} \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation}\: \\ $$$$\left(\mathrm{1}−{q}+\frac{{p}^{\mathrm{2}} }{\mathrm{2}}\right){x}^{\mathrm{2}} +{p}\left(\mathrm{1}+{q}\right){x}+{q}\left({q}−\mathrm{1}\right)+\frac{{p}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{equal}\:\mathrm{roots},\:\mathrm{prove}\:\mathrm{that}\:{p}^{\mathrm{2}} =\mathrm{4}{q} \\ $$

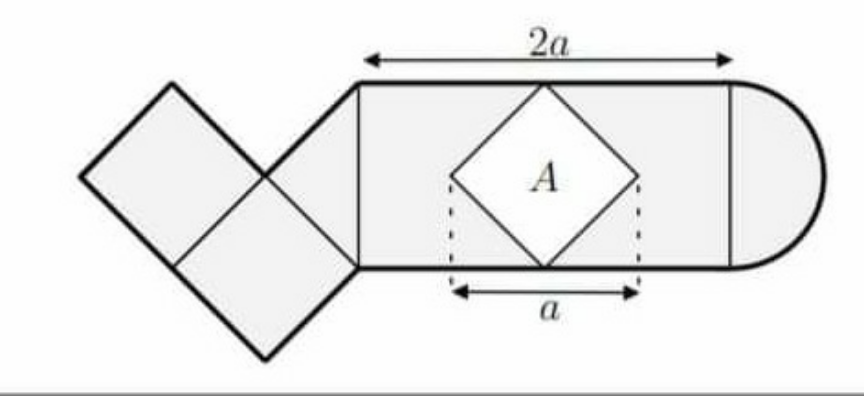
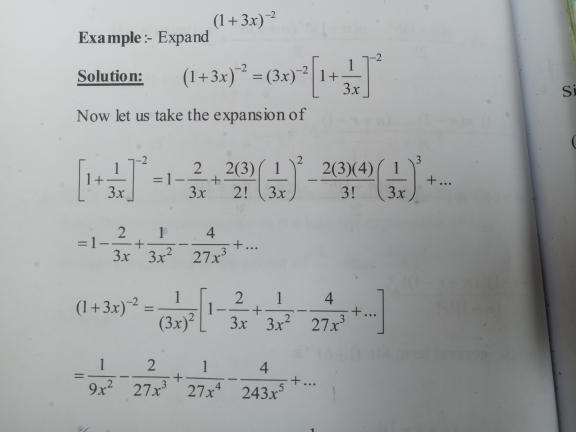
Question Number 113682 Answers: 8 Comments: 1

Question Number 113675 Answers: 1 Comments: 3

Pg 1043 Pg 1044 Pg 1045 Pg 1046 Pg 1047 Pg 1048 Pg 1049 Pg 1050 Pg 1051 Pg 1052

Contact: info@tinkutara.com