Question and Answers Forum

AllQuestion and Answers: Page 1046

Question Number 114635 Answers: 1 Comments: 3

find ∫_0 ^1 x^4 ln(x)ln(1−x^2 )dx

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\: \\ $$

Question Number 114627 Answers: 2 Comments: 0

sin A+sin 2A+sin 3A+...+sin nA =??

$$\mathrm{sin}\:{A}+\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{3}{A}+...+\mathrm{sin}\:{nA}\:=?? \\ $$

Question Number 114625 Answers: 1 Comments: 0

Question Number 114615 Answers: 1 Comments: 0

Question Number 114597 Answers: 3 Comments: 0

What is the number value of f[((log((( (√(x )) − 1 )/(x − 1))) ))^(1/3) ] = (√((√(x )) + x )) for f(−1)? a) 0,1 b) 27 c) 81 d) 10 e) 12

Question Number 114593 Answers: 1 Comments: 0

((∣x−1∣)/(∣x∣−1)) ≤ 1

$$\frac{\mid{x}−\mathrm{1}\mid}{\mid{x}\mid−\mathrm{1}}\:\leqslant\:\mathrm{1} \\ $$

Question Number 114592 Answers: 3 Comments: 0

Solve : x^2 +2x−1≡0(mod 3)

$$\mathrm{Solve}\::\:{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$

Question Number 114586 Answers: 1 Comments: 2

f(x)−2f((1/2))=3x−2 f(x)=?

$$\mathrm{f}\left(\mathrm{x}\right)−\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{3x}−\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=? \\ $$

Question Number 114582 Answers: 0 Comments: 1

Question Number 114577 Answers: 1 Comments: 5

x=(π/(30)) ((cos14x×cos6x)/(cos4x))=?

$$\mathrm{x}=\frac{\pi}{\mathrm{30}} \\ $$$$\frac{\mathrm{cos14x}×\mathrm{cos6x}}{\mathrm{cos4x}}=? \\ $$

Question Number 114570 Answers: 2 Comments: 0

Given that N=625(1−(9/5^2 ))(1−(9/8^2 ))(1−(9/(11^2 )))...(1−(9/(125^2 ))) Find the sum of the digits of N.

$$\mathrm{Given}\:\mathrm{that}\: \\ $$$${N}=\mathrm{625}\left(\mathrm{1}−\frac{\mathrm{9}}{\mathrm{5}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{9}}{\mathrm{8}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{\mathrm{9}}{\mathrm{11}^{\mathrm{2}} }\right)...\left(\mathrm{1}−\frac{\mathrm{9}}{\mathrm{125}^{\mathrm{2}} }\right) \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{of}\:{N}. \\ $$

Question Number 114567 Answers: 0 Comments: 1

Question Number 114566 Answers: 2 Comments: 0

Question Number 114561 Answers: 1 Comments: 0

Question Number 114554 Answers: 1 Comments: 0

Given a matrix A = (((a b)),((c d)) ) satisfies the equation A^2 +λA+7I = 0 where I= (((1 0)),((0 1)) ) . Find the value of trace of A

$${Given}\:{a}\:{matrix}\:{A}\:=\:\begin{pmatrix}{{a}\:\:\:{b}}\\{{c}\:\:\:{d}}\end{pmatrix}\:{satisfies} \\ $$$${the}\:{equation}\:{A}^{\mathrm{2}} +\lambda{A}+\mathrm{7}{I}\:=\:\mathrm{0} \\ $$$${where}\:{I}=\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\:.\:{Find}\:{the}\:{value}\:{of}\: \\ $$$${trace}\:{of}\:{A}\: \\ $$

Question Number 114551 Answers: 1 Comments: 3

The value of x in the given equation 4^x −3^(x−(1/2)) = 3^(x+(1/2)) −2^(2x−1) , is _,

$${The}\:{value}\:{of}\:{x}\:{in}\:{the}\:{given}\:{equation} \\ $$$$\mathrm{4}^{{x}} −\mathrm{3}^{{x}−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\mathrm{3}^{{x}+\frac{\mathrm{1}}{\mathrm{2}}} \:−\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} \:,\:{is}\:\_, \\ $$

Question Number 114543 Answers: 2 Comments: 0

lim_(x→0) ((x^2 arctan (2x))/(x cos x+tan x)) ?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \:\mathrm{arctan}\:\left(\mathrm{2}{x}\right)}{{x}\:\mathrm{cos}\:{x}+\mathrm{tan}\:{x}}\:? \\ $$

Question Number 114541 Answers: 1 Comments: 0

Question Number 114539 Answers: 2 Comments: 1

lim_(x→0) [ ((sinh x − sin x)/x^3 ) ] = ?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left[\:\frac{\mathrm{sinh}\:{x}\:−\:\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\:\right]\:\:=\:\:? \\ $$

Question Number 114538 Answers: 1 Comments: 4

how many trees can be planted in one square meter area if the distance between each tow trees is 3cm?

$${how}\:{many}\:{trees}\:{can}\:{be}\:{planted}\:{in}\:{one} \\ $$$${square}\:{meter}\:{area}\:{if}\:{the}\:{distance}\: \\ $$$${between}\:{each}\:{tow}\:{trees}\:{is}\:\mathrm{3}{cm}? \\ $$

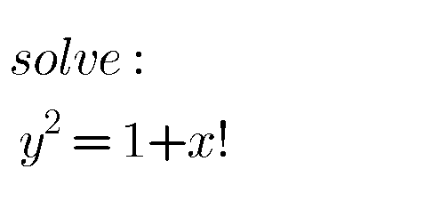
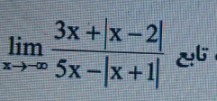
Question Number 114536 Answers: 0 Comments: 2

Question Number 114533 Answers: 1 Comments: 0

Question Number 114526 Answers: 1 Comments: 2

(1/π)∫_0 ^π e^(2cos θ) dθ ?

$$\frac{\mathrm{1}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}\:{e}^{\mathrm{2cos}\:\theta} \:{d}\theta\:? \\ $$

Question Number 114514 Answers: 1 Comments: 2

Question Number 114512 Answers: 1 Comments: 4

Question Number 114511 Answers: 2 Comments: 3

Find numbers which are common terms of the two following arithmetic progression: 3,7,11,...,407 and 2,9,16,...,709

$$\mathrm{Find}\:\mathrm{numbers}\:\mathrm{which}\:\mathrm{are}\:\mathrm{common} \\ $$$$\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two}\:\mathrm{following}\:\mathrm{arithmetic} \\ $$$$\mathrm{progression}: \\ $$$$\mathrm{3},\mathrm{7},\mathrm{11},...,\mathrm{407}\:\mathrm{and}\:\mathrm{2},\mathrm{9},\mathrm{16},...,\mathrm{709} \\ $$

Pg 1041 Pg 1042 Pg 1043 Pg 1044 Pg 1045 Pg 1046 Pg 1047 Pg 1048 Pg 1049 Pg 1050

Contact: info@tinkutara.com