
AllQuestion and Answers: Page 1040
Question Number 115829 Answers: 1 Comments: 0
Question Number 115750 Answers: 4 Comments: 0

Question Number 115743 Answers: 3 Comments: 0
$$\int\:{e}^{{ax}} .\mathrm{sin}\:{bx}\:{dx}\:=? \\ $$$${by}\:{complex}\:{number} \\ $$
Question Number 115742 Answers: 1 Comments: 0
Question Number 115736 Answers: 2 Comments: 0

Question Number 115733 Answers: 3 Comments: 0
Question Number 115732 Answers: 0 Comments: 1

Question Number 115725 Answers: 1 Comments: 0
Question Number 115721 Answers: 2 Comments: 4
Question Number 115714 Answers: 0 Comments: 1
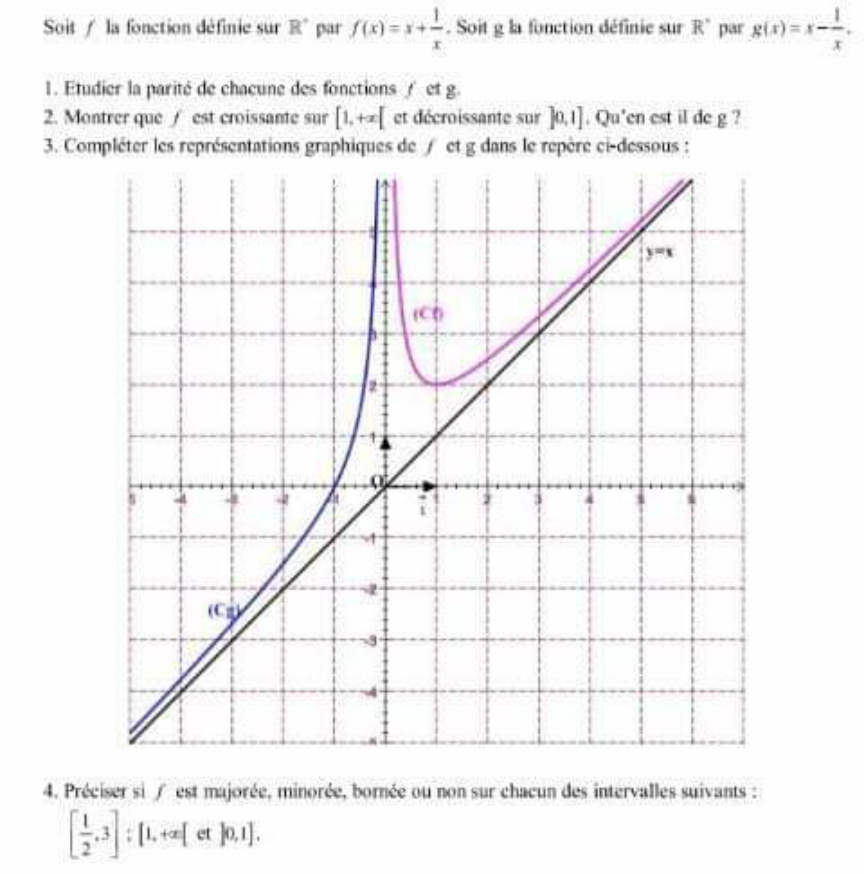
Question Number 115706 Answers: 1 Comments: 3
Question Number 115705 Answers: 1 Comments: 0
Question Number 115711 Answers: 2 Comments: 0
Question Number 115696 Answers: 0 Comments: 4
Question Number 115695 Answers: 2 Comments: 0
Question Number 115689 Answers: 1 Comments: 0

Question Number 115685 Answers: 1 Comments: 0
Question Number 115674 Answers: 1 Comments: 0
Question Number 115664 Answers: 2 Comments: 0
Question Number 115661 Answers: 2 Comments: 0
Question Number 115683 Answers: 1 Comments: 0
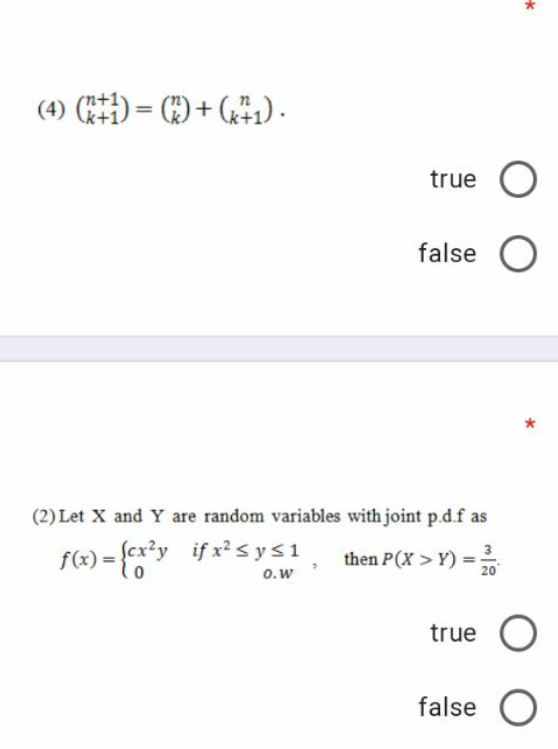
Question Number 115656 Answers: 3 Comments: 1
$$\int\:\sqrt{\frac{{x}−{a}}{{b}−{x}}}\:{dx}\:=\:? \\ $$$${where}\:{a}\:<{x}\:<\:{b} \\ $$
Question Number 115653 Answers: 0 Comments: 1

Question Number 115646 Answers: 1 Comments: 3

Question Number 115645 Answers: 1 Comments: 2

Question Number 115643 Answers: 0 Comments: 0

Pg 1035 Pg 1036 Pg 1037 Pg 1038 Pg 1039 Pg 1040 Pg 1041 Pg 1042 Pg 1043 Pg 1044
