Question and Answers Forum

AllQuestion and Answers: Page 1038

Question Number 116006 Answers: 1 Comments: 0

3(sin x−cos x)^4 +6(sin x+cos x)^2 +4(sin^6 x+cos^6 x) = _____.

$$\mathrm{3}\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)^{\mathrm{4}} +\mathrm{6}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}\left(\mathrm{sin}^{\mathrm{6}} {x}+\mathrm{cos}^{\mathrm{6}} {x}\right)\:=\:\_\_\_\_\_. \\ $$

Question Number 116005 Answers: 0 Comments: 0

... advanced mathematics... prove that::: lim_(x→1^+ ) ( ζ( x ) −(1/(x − 1))) =^(???) γ γ:: Euler − mascheroni constant. m.n.huly 1970

$$\:\:\:\:\:\:\:\:\:...\:{advanced}\:\:{mathematics}... \\ $$$$ \\ $$$$\:\:\:\:\:{prove}\:\:{that}::: \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{lim}_{{x}\rightarrow\mathrm{1}^{+} } \left(\:\zeta\left(\:{x}\:\right)\:−\frac{\mathrm{1}}{{x}\:−\:\mathrm{1}}\right)\:\overset{???} {=}\gamma\:\:\: \\ $$$$\:\:\gamma::\:\mathscr{E}{uler}\:−\:{mascheroni}\:{constant}. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.{huly}\:\mathrm{1970} \\ $$$$ \\ $$

Question Number 116000 Answers: 0 Comments: 0

U(n)=∫_0 ^∞ ((1−tanh x)/( ((tanh x))^(1/n) ))dx another way?

$${U}\left({n}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\mathrm{tanh}\:{x}}{\:\sqrt[{{n}}]{\mathrm{tanh}\:{x}}}{dx} \\ $$$${another}\:{way}? \\ $$$$ \\ $$

Question Number 115999 Answers: 1 Comments: 0

lim_(x→0) ((1−cos x (√(cos 2x)) ((cos 3x))^(1/(3 )) ((cos 4x))^(1/(4 )) )/x^2 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{cos}\:\mathrm{3}{x}}\:\sqrt[{\mathrm{4}\:}]{\mathrm{cos}\:\mathrm{4}{x}}}{{x}^{\mathrm{2}} } \\ $$

Question Number 115997 Answers: 1 Comments: 0

Question Number 115988 Answers: 1 Comments: 2

Question Number 115986 Answers: 1 Comments: 0

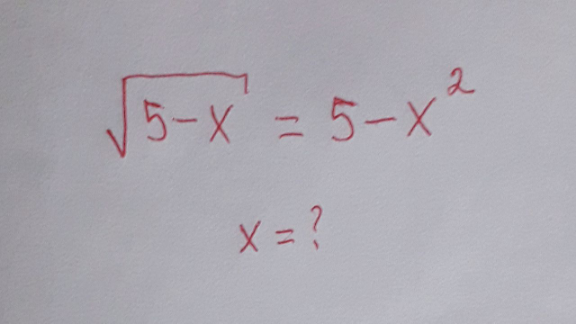
Question Number 115974 Answers: 0 Comments: 0

∫((e^(3x) −e^x )/(x(e^(3x) +1)(e^x +1)))dx = ?

$$\int\frac{{e}^{\mathrm{3}{x}} −{e}^{{x}} }{{x}\left({e}^{\mathrm{3}{x}} +\mathrm{1}\right)\left({e}^{{x}} +\mathrm{1}\right)}{dx}\:=\:? \\ $$

Question Number 115968 Answers: 1 Comments: 0

Question Number 115961 Answers: 2 Comments: 8

Question Number 115960 Answers: 0 Comments: 1

f^2 (x)=f(2x)+2f(x)−2 f(1)=3 ⇒ f(6)=?

$${f}^{\mathrm{2}} \left({x}\right)={f}\left(\mathrm{2}{x}\right)+\mathrm{2}{f}\left({x}\right)−\mathrm{2}\: \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{3}\:\:\:\Rightarrow\:{f}\left(\mathrm{6}\right)=? \\ $$

Question Number 115951 Answers: 1 Comments: 0

x,y,z ε R^+ 2x+3y+4z=1 ⇒ (1/x)+(1/y)+(1/z) smallest integer value?

$${x},{y},{z}\:\epsilon\:{R}^{+} \:\: \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{4}{z}=\mathrm{1}\:\:\Rightarrow\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\:{smallest}\:{integer}\:{value}?\: \\ $$

Question Number 115943 Answers: 4 Comments: 4

Question Number 115940 Answers: 0 Comments: 0

solve ∫_0 ^1 ((ln^2 (1−x))/(1+x^2 ))dx

$${solve} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 115927 Answers: 2 Comments: 0

calculate ∫_1 ^(+∞) (dx/((4x^2 −1)^3 ))

$$\mathrm{calculate}\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Question Number 115946 Answers: 1 Comments: 0

Given that the sum of infinity of geometric series a−2ar+4ar^2 −8ar^3 +...a(−2r)^(n−1) +...is 3 and the sum of infinity of geometric series a+ar+ar^2 +ar^3 +...ar^(n−1) +... is k, find the range of values of k.

$$\mathrm{Given}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{infinity}\:\mathrm{of}\:\mathrm{geometric} \\ $$$$\mathrm{series}\:{a}−\mathrm{2}{ar}+\mathrm{4}{ar}^{\mathrm{2}} −\mathrm{8}{ar}^{\mathrm{3}} +...{a}\left(−\mathrm{2}{r}\right)^{{n}−\mathrm{1}} \:+...\mathrm{is}\:\mathrm{3} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{infinity}\:\mathrm{of}\:\mathrm{geometric}\:\mathrm{series} \\ $$$${a}+{ar}+{ar}^{\mathrm{2}} +{ar}^{\mathrm{3}} +...{ar}^{{n}−\mathrm{1}} +...\:\mathrm{is}\:{k},\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:{k}. \\ $$

Question Number 115922 Answers: 1 Comments: 0

find the stationary points of the function U=x^2 +y^2 subjects to the constraint x^2 +y^2 +2x−2y+1=0

$${find}\:{the}\:{stationary}\:{points}\:{of}\:{the} \\ $$$${function}\:{U}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:{subjects}\:{to} \\ $$$${the}\:{constraint}\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0} \\ $$

Question Number 115932 Answers: 2 Comments: 0

13^(14) ÷4 Remaining?

$$\mathrm{13}^{\mathrm{14}} \boldsymbol{\div}\mathrm{4} \\ $$$$\mathrm{Remaining}? \\ $$

Question Number 115920 Answers: 4 Comments: 0

prove that :: ∫_0 ^( ∞) (tanh^a (x) −tanh^b (x))dx =^(???) ((ψ(((b+1)/2))−ψ(((a+1)/2)))/2) m.n.july.1970

$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:{prove}\:\:\:{that}\::: \\ $$$$\: \\ $$$$\:\int_{\mathrm{0}} ^{\:\infty} \left({tanh}^{{a}} \left({x}\right)\:−{tanh}^{{b}} \left({x}\right)\right){dx}\: \\ $$$$\:\:\:\:\:\:\overset{???} {=}\:\:\:\frac{\psi\left(\frac{{b}+\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{m}.{n}.{july}.\mathrm{1970} \\ $$$$\: \\ $$

Question Number 115935 Answers: 0 Comments: 0

Question Number 115934 Answers: 0 Comments: 0

Question Number 115916 Answers: 1 Comments: 0

Question Number 115910 Answers: 0 Comments: 1

let x be a posative real number prove that Σ_(n=1) ^∞ (((n−1)!)/((x+1)....(x+n)))=(1/x)

$${let}\:{x}\:{be}\:{a}\:{posative}\:{real}\:{number} \\ $$$${prove}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({n}−\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)....\left({x}+{n}\right)}=\frac{\mathrm{1}}{{x}} \\ $$

Question Number 115909 Answers: 1 Comments: 0

solve the system of equations x+((3x−y)/(x^2 +y^2 ))=3 , y−((x+3y)/(x^2 +y^2 ))=0

$${solve}\:{the}\:{system}\:{of}\:{equations} \\ $$$${x}+\frac{\mathrm{3}{x}−{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\mathrm{3}\:,\:{y}−\frac{{x}+\mathrm{3}{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\mathrm{0} \\ $$

Question Number 115908 Answers: 1 Comments: 2

what is the cofficient of x^2 (1+x)(1+2x)(1+4x)......(1+2^n x)

$${what}\:{is}\:{the}\:{cofficient}\:{of}\:{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{1}+\mathrm{4}{x}\right)......\left(\mathrm{1}+\mathrm{2}^{{n}} {x}\right) \\ $$

Question Number 115906 Answers: 1 Comments: 0

find all pairs of integers (x,y) such that x^3 +y^3 =(x+y)^2

$${find}\:{all}\:{pairs}\:{of}\:{integers}\:\left({x},{y}\right)\:{such}\:{that} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\left({x}+{y}\right)^{\mathrm{2}} \\ $$

Pg 1033 Pg 1034 Pg 1035 Pg 1036 Pg 1037 Pg 1038 Pg 1039 Pg 1040 Pg 1041 Pg 1042

Contact: info@tinkutara.com