Question and Answers Forum

AllQuestion and Answers: Page 1037

Question Number 115332 Answers: 4 Comments: 3

Minimum value of function f(x)= ((16x^2 cos^2 x+4)/(x cos x)) where −π<x<0

$${Minimum}\:{value}\:{of}\:{function}\: \\ $$$${f}\left({x}\right)=\:\frac{\mathrm{16}{x}^{\mathrm{2}} \:\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{4}}{{x}\:\mathrm{cos}\:{x}}\:{where}\:−\pi<{x}<\mathrm{0} \\ $$

Question Number 115328 Answers: 1 Comments: 0

If ((sin 1°+sin 2°+sin 3°+...+sin 44°)/(cos 1°+cos 2°+cos 3°+...+cos 44°))=χ then χ^4 +4χ^3 +4χ^2 +4=

$${If}\:\frac{\mathrm{sin}\:\mathrm{1}°+\mathrm{sin}\:\mathrm{2}°+\mathrm{sin}\:\mathrm{3}°+...+\mathrm{sin}\:\mathrm{44}°}{\mathrm{cos}\:\mathrm{1}°+\mathrm{cos}\:\mathrm{2}°+\mathrm{cos}\:\mathrm{3}°+...+\mathrm{cos}\:\mathrm{44}°}=\chi \\ $$$${then}\:\chi^{\mathrm{4}} +\mathrm{4}\chi^{\mathrm{3}} +\mathrm{4}\chi^{\mathrm{2}} +\mathrm{4}= \\ $$

Question Number 115325 Answers: 0 Comments: 5

Question Number 115320 Answers: 4 Comments: 0

(1)lim_(x→0) ((1−cos^6 (2x)cos^3 (3x))/(3x^2 )) ? (2)lim_(x→0) ((1−cos 4x+2sin^2 x.cos 4x)/(x^2 .cos 3x))? (3) lim_(x→(π/2)) ((sin x−2cos^2 x−1)/( (√(sin^3 x))−(√(sin x)))) ?

$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{6}} \left(\mathrm{2}{x}\right)\mathrm{cos}\:^{\mathrm{3}} \left(\mathrm{3}{x}\right)}{\mathrm{3}{x}^{\mathrm{2}} }\:? \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:\mathrm{4}{x}}{{x}^{\mathrm{2}} .\mathrm{cos}\:\mathrm{3}{x}}? \\ $$$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}}−\sqrt{\mathrm{sin}\:{x}}}\:?\: \\ $$

Question Number 115318 Answers: 2 Comments: 0

lim_(x→0) ((xsin x)/(2sin^2 (3x)−x^2 cos x))

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\mathrm{sin}\:{x}}{\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)−{x}^{\mathrm{2}} \mathrm{cos}\:{x}} \\ $$

Question Number 115312 Answers: 3 Comments: 2

Solve for x ∈ R that suitable on this inequality : (√(8−x^2 )) > x

$${Solve}\:\:{for}\:\:{x}\:\in\:\mathbb{R}\:\:{that}\:\:{suitable}\:\:{on}\:\:{this} \\ $$$${inequality}\::\:\:\:\:\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }\:\:>\:\:{x} \\ $$

Question Number 115302 Answers: 1 Comments: 0

... nice math... find lim_(n→∞ ) {Σ_(k=1) ^n ∫_(k−1) ^( k) tan^(−1) (((nx−nk)/(kx+n^2 )))dx}

$$\:\:\:\:\:\:\:...\:{nice}\:\:{math}... \\ $$$$\:\:\:\:\:{find} \\ $$$$\:\:\:\:{lim}_{{n}\rightarrow\infty\:\:} \left\{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{{k}−\mathrm{1}} ^{\:\:{k}} {tan}^{−\mathrm{1}} \left(\frac{{nx}−{nk}}{{kx}+{n}^{\mathrm{2}} }\right){dx}\right\} \\ $$$$\: \\ $$

Question Number 115301 Answers: 2 Comments: 0

if jx^2 +2kxy+by^2 =1 show that (kx+by)^3 (d^2 y/dx^2 )=k^2 −jb

$${if}\: \\ $$$${jx}^{\mathrm{2}} +\mathrm{2}{kxy}+{by}^{\mathrm{2}} =\mathrm{1}\:{show}\:{that} \\ $$$$\left({kx}+{by}\right)^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={k}^{\mathrm{2}} −{jb} \\ $$

Question Number 115300 Answers: 1 Comments: 0

find from fourier series an expression for log(tanx)

$${find}\:{from}\:{fourier}\:{series}\:{an} \\ $$$${expression}\:{for} \\ $$$$\mathrm{log}\left(\mathrm{tan}{x}\right) \\ $$

Question Number 115298 Answers: 1 Comments: 2

(d^2 y/dx^2 )+log(y)=0

$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{log}\left(\mathrm{y}\right)=\mathrm{0} \\ $$

Question Number 115294 Answers: 2 Comments: 0

Given that N=1×2×3×...×500 is the product of the positive integers from 1 to 500. If N is divisible by 6^k , find the largest possible value of k.

$$\mathrm{Given}\:\mathrm{that}\:{N}=\mathrm{1}×\mathrm{2}×\mathrm{3}×...×\mathrm{500}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{product}\:\mathrm{of}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{500}. \\ $$$$ \\ $$$$\mathrm{If}\:{N}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{6}^{{k}} ,\:\mathrm{find}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{possible} \\ $$$$\mathrm{value}\:\mathrm{of}\:{k}. \\ $$

Question Number 115285 Answers: 0 Comments: 0

...♠nice topology ♠... suppose ⟨S , τ ⟩ is Baire′s space and S = ∪_(n=1) ^∞ F_n such that F_n ′s are closed sets prove that:: ∃ m ; F_m ^( °) ≠ ∅ ..m.n.july ...♣m.n.july.1970♣...

$$\:\:\:\:\:\:\:\:...\spadesuit{nice}\:\:\:{topology}\:\spadesuit... \\ $$$${suppose}\:\:\langle{S}\:,\:\tau\:\rangle\:{is}\:\:{Baire}'{s} \\ $$$${space}\:\:\:{and}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\cup}}{F}_{{n}} \:\:\:{such} \\ $$$${that}\:\:{F}_{{n}} '{s}\:\:{are}\:{closed}\:{sets}\: \\ $$$$\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\exists\:{m}\:;\:{F}_{{m}} ^{\:°} \:\neq\:\varnothing\:\:\:..{m}.{n}.{july} \\ $$$$\:\:\:\:\:\:\:\:\:...\clubsuit{m}.{n}.{july}.\mathrm{1970}\clubsuit... \\ $$

Question Number 115273 Answers: 2 Comments: 0

... advanced mathematics... evaluate::: Δ=∫_0 ^( ∞) ((cos(ln(x)))/((x+1)^2 )) dx =??? ...m.n.july.1970...

$$\:\:\:\:\:\:\:\:...\:{advanced}\:\:{mathematics}... \\ $$$$ \\ $$$$\:\:\:\:\:{evaluate}::: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Delta=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{cos}\left({ln}\left({x}\right)\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:=??? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$$$\: \\ $$

Question Number 115268 Answers: 1 Comments: 0

(√(4^x −5.2^(x+1) +25)) +(√(9^x −2.3^(x+2) +17)) ≤ 2^x −5

$$\sqrt{\mathrm{4}^{{x}} −\mathrm{5}.\mathrm{2}^{{x}+\mathrm{1}} +\mathrm{25}}\:+\sqrt{\mathrm{9}^{{x}} −\mathrm{2}.\mathrm{3}^{{x}+\mathrm{2}} +\mathrm{17}}\:\leqslant\:\mathrm{2}^{{x}} −\mathrm{5} \\ $$

Question Number 115267 Answers: 1 Comments: 0

If f(x) is a differentiable function defined ∀x∈R such that (f(x))^3 −x+f(x)=0 then ∫_0 ^(√2) f^(−1) (x) dx =

$${If}\:{f}\left({x}\right)\:{is}\:{a}\:{differentiable}\:{function} \\ $$$${defined}\:\:\forall{x}\in\mathbb{R}\:{such}\:{that}\:\left({f}\left({x}\right)\right)^{\mathrm{3}} −{x}+{f}\left({x}\right)=\mathrm{0} \\ $$$${then}\:\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{2}}} {\int}}\:{f}^{−\mathrm{1}} \left({x}\right)\:{dx}\:=\: \\ $$

Question Number 115261 Answers: 2 Comments: 0

Equation of circle touching the line ∣x−2∣+∣y−3∣ = 4 will be

$${Equation}\:{of}\:{circle}\:{touching}\:{the}\:{line}\: \\ $$$$\mid{x}−\mathrm{2}\mid+\mid{y}−\mathrm{3}\mid\:=\:\mathrm{4}\:{will}\:{be}\: \\ $$

Question Number 115260 Answers: 2 Comments: 1

Let f be a real valued function defined on the interval (−1,1) such that e^(−x) .f(x)=2+∫_0 ^x (√(t^4 +1)) dt ∀x∈(−1,1) and let g be the inverse function of f . Find the value of g′(2).

$${Let}\:{f}\:{be}\:{a}\:{real}\:{valued}\:{function}\:{defined} \\ $$$${on}\:{the}\:{interval}\:\left(−\mathrm{1},\mathrm{1}\right)\:{such}\:{that}\: \\ $$$${e}^{−{x}} .{f}\left({x}\right)=\mathrm{2}+\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}\:{dt}\:\forall{x}\in\left(−\mathrm{1},\mathrm{1}\right) \\ $$$${and}\:{let}\:{g}\:{be}\:{the}\:{inverse}\:{function}\:{of}\:{f} \\ $$$$.\:{Find}\:{the}\:{value}\:{of}\:{g}'\left(\mathrm{2}\right). \\ $$

Question Number 115258 Answers: 1 Comments: 0

A vector of magnitude 2 along a bisector of the angle between the two vectors 2i^ −2j^ +k^ and i^ +2j^ −2k^ is __

$${A}\:{vector}\:{of}\:{magnitude}\:\mathrm{2}\:{along}\:{a}\:{bisector} \\ $$$${of}\:{the}\:{angle}\:{between}\:{the}\:{two}\:{vectors} \\ $$$$\mathrm{2}\hat {{i}}−\mathrm{2}\hat {{j}}+\hat {{k}}\:{and}\:\hat {{i}}+\mathrm{2}\hat {{j}}−\mathrm{2}\hat {{k}}\:{is}\:\_\_ \\ $$

Question Number 115255 Answers: 0 Comments: 0

Express cosec 3x in terms of cosec x.

$$\mathrm{Express}\:\mathrm{cosec}\:\mathrm{3x}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{cosec}\:\mathrm{x}. \\ $$

Question Number 115253 Answers: 1 Comments: 0

Express sin 4x interm of sin x.

$$\mathrm{Express}\:\mathrm{sin}\:\mathrm{4x}\:\mathrm{interm}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{x}. \\ $$

Question Number 115250 Answers: 0 Comments: 0

If mr Fosu sells the car after covering a mileage of 128km. find the i. value of the car if the rate of depreciation is $ 0.03 per km ii. the range of values for which Mr Fosu could sell the car so that he does not lose more than $,2000 or gain more tban $3,000 on the depreciated value.

$$\mathrm{If}\:\mathrm{mr}\:\mathrm{Fosu}\:\mathrm{sells}\:\mathrm{the}\:\mathrm{car}\:\mathrm{after}\:\mathrm{covering}\: \\ $$$$\mathrm{a}\:\mathrm{mileage}\:\mathrm{of}\:\mathrm{128km}.\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{i}.\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{car}\:\mathrm{if}\:\mathrm{the}\:\mathrm{rate}\:\mathrm{of}\: \\ $$$$\mathrm{depreciation}\:\mathrm{is}\:\$\:\mathrm{0}.\mathrm{03}\:\mathrm{per}\:\mathrm{km} \\ $$$$\mathrm{ii}.\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{values}\:\mathrm{for}\:\mathrm{which}\:\mathrm{Mr} \\ $$$$\mathrm{Fosu}\:\mathrm{could}\:\mathrm{sell}\:\mathrm{the}\:\mathrm{car}\:\mathrm{so}\:\mathrm{that}\:\mathrm{he}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{lose}\:\mathrm{more}\:\mathrm{than}\:\$,\mathrm{2000}\:\mathrm{or}\:\mathrm{gain}\:\mathrm{more}\:\mathrm{tban}\: \\ $$$$\$\mathrm{3},\mathrm{000}\:\mathrm{on}\:\mathrm{the}\:\mathrm{depreciated}\:\mathrm{value}. \\ $$

Question Number 115248 Answers: 1 Comments: 0

Express cos 4x interm of cos x.

$$\mathrm{Express}\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{interm}\:\mathrm{of}\:\mathrm{cos}\:\mathrm{x}. \\ $$

Question Number 115246 Answers: 0 Comments: 1

5^((x+1)^2 ) + 625 ≤ 5^(x^2 +2) + 5^(2x+3)

$$\:\:\:\:\mathrm{5}^{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \:+\:\mathrm{625}\:\leqslant\:\mathrm{5}^{{x}^{\mathrm{2}} +\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}{x}+\mathrm{3}} \\ $$

Question Number 115238 Answers: 2 Comments: 0

64^(x^2 −(3/4)x) ≤ ((√8))^x^3

$$\:\:\:\mathrm{64}^{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}} \:\leqslant\:\left(\sqrt{\mathrm{8}}\right)^{{x}^{\mathrm{3}} } \: \\ $$

Question Number 115237 Answers: 2 Comments: 0

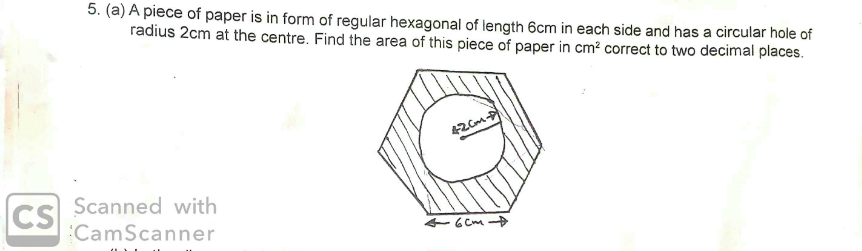
Question Number 115230 Answers: 0 Comments: 6

2 women and 4 men will sit on the 8 available seats and surround the round table . The many possible arrangements of them sitting if they sat randomly

$$\mathrm{2}\:{women}\:{and}\:\mathrm{4}\:{men}\:{will}\:{sit}\:{on}\:{the} \\ $$$$\mathrm{8}\:{available}\:{seats}\:{and}\:{surround}\: \\ $$$${the}\:{round}\:{table}\:.\:{The}\:{many}\:{possible} \\ $$$${arrangements}\:{of}\:{them}\:{sitting} \\ $$$${if}\:{they}\:{sat}\:{randomly} \\ $$

Pg 1032 Pg 1033 Pg 1034 Pg 1035 Pg 1036 Pg 1037 Pg 1038 Pg 1039 Pg 1040 Pg 1041

Contact: info@tinkutara.com