Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1035

Question Number 114768 Answers: 2 Comments: 0

Solve for ∣x−2∣+∣1−x∣=4

$$\mathrm{Solve}\:\mathrm{for}\:\mid{x}−\mathrm{2}\mid+\mid\mathrm{1}−{x}\mid=\mathrm{4} \\ $$

Question Number 114765 Answers: 1 Comments: 0

Find the maximum. and minimum value of ⌊1+sinx⌋+⌊1+sin3x⌋+⌊1+sin2x⌋

$${Find}\:{the}\:\boldsymbol{{maximum}}.\:{and}\:\boldsymbol{{minimum}}\:{value}\:{of}\:\lfloor\mathrm{1}+{sinx}\rfloor+\lfloor\mathrm{1}+{sin}\mathrm{3}{x}\rfloor+\lfloor\mathrm{1}+{sin}\mathrm{2}{x}\rfloor \\ $$$$ \\ $$$$ \\ $$

Question Number 114764 Answers: 1 Comments: 0

Find period of f(x)=e^(cos^4 (πx)+x−⌊x⌋+cos^2 (πx))

$${Find}\:{period}\:{of}\:{f}\left({x}\right)={e}^{{cos}^{\mathrm{4}} \left(\pi{x}\right)+{x}−\lfloor{x}\rfloor+{cos}^{\mathrm{2}} \left(\pi{x}\right)} \\ $$$$ \\ $$

Question Number 114758 Answers: 1 Comments: 0

Π_(n=1) ^∞ ((4n^2 (10n−6)(10n−4))/((2n−1)^2 (10n−1)(10n+1))) =?

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\:\frac{\mathrm{4}{n}^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{6}\right)\left(\mathrm{10}{n}−\mathrm{4}\right)}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{10}{n}−\mathrm{1}\right)\left(\mathrm{10}{n}+\mathrm{1}\right)}\:=? \\ $$

Question Number 114754 Answers: 4 Comments: 1

Without L′Hopital lim_(x→(π/4)) ((((1/(cos^2 x)) −2tan x ))/(cos 2x)) ?

$${Without}\:{L}'{Hopital}\: \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:−\mathrm{2tan}\:{x}\:\right)}{\mathrm{cos}\:\mathrm{2}{x}}\:? \\ $$

Question Number 114753 Answers: 1 Comments: 0

find minimum value of function f(x) = (((x+17)^3 )/x) , x>0

$${find}\:{minimum}\:{value}\:{of}\:{function} \\ $$$${f}\left({x}\right)\:=\:\frac{\left({x}+\mathrm{17}\right)^{\mathrm{3}} }{{x}}\:,\:{x}>\mathrm{0} \\ $$

Question Number 114740 Answers: 2 Comments: 0

question proposed by m.n july 1970 show that ∫_0 ^∞ ((ln(1+x))/(x(1+x^2 )))dx=((5π^2 )/(48))

$${question}\:{proposed}\:{by}\:{m}.{n}\:{july}\:\mathrm{1970} \\ $$$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$

Question Number 114739 Answers: 1 Comments: 0

find the largest and smallest coefficient in (4+3x)^(−5) .

$${find}\:{the}\:{largest}\:{and}\:{smallest} \\ $$$${coefficient}\:{in}\:\left(\mathrm{4}+\mathrm{3}{x}\right)^{−\mathrm{5}} . \\ $$

Question Number 114735 Answers: 1 Comments: 0

.... nice mathematics... prove that:: Σ_(n=1) ^∞ (([ (((2n)),(n) )]^2 )/((2n−1)2^(4n) )) =1−(2/π) ... m.n.july. 1970#

$$\:\:\:....\:{nice}\:\:{mathematics}... \\ $$$$ \\ $$$$\:\:{prove}\:\:{that}::\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left[\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}\right]^{\mathrm{2}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\mathrm{2}^{\mathrm{4}{n}} }\:=\mathrm{1}−\frac{\mathrm{2}}{\pi}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{m}.{n}.{july}.\:\mathrm{1970}# \\ $$

Question Number 114728 Answers: 0 Comments: 2

(3+4x)^(−5) =3^(−5) ×(1+(4/3)x)^(−5) ... pls what is the explanation behind the fact that i always have to factorize to get the form (1+b)^(−s) any time i am solving for binomial with negatuve power? can it be solved without first factorizing?

$$ \\ $$$$\left(\mathrm{3}+\mathrm{4}{x}\right)^{−\mathrm{5}} \\ $$$$=\mathrm{3}^{−\mathrm{5}} ×\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{3}}{x}\right)^{−\mathrm{5}} \\ $$$$... \\ $$$${pls}\:{what}\:{is}\:{the}\:{explanation}\:{behind}\:{the}\:{fact} \\ $$$${that}\:{i}\:{always}\:{have}\:{to}\:{factorize}\:{to}\:{get}\:{the}\:{form} \\ $$$$\left(\mathrm{1}+{b}\right)^{−{s}} \:{any}\:{time}\:{i}\:{am}\:{solving}\:{for}\:{binomial} \\ $$$${with}\:{negatuve}\:{power}? \\ $$$${can}\:{it}\:{be}\:{solved}\:{without}\:{first}\:{factorizing}? \\ $$

Question Number 114722 Answers: 2 Comments: 0

a_n (d^n Ψ/dt^n )+a_(n−1) (d^(n−1) Ψ/dt^(n−1) )+.....+a_1 (dΨ/dt)+a_0 Ψ=0 Is it solvable???

$${a}_{{n}} \frac{{d}^{{n}} \Psi}{{dt}^{{n}} }+{a}_{{n}−\mathrm{1}} \frac{{d}^{{n}−\mathrm{1}} \Psi}{{dt}^{{n}−\mathrm{1}} }+.....+{a}_{\mathrm{1}} \frac{{d}\Psi}{{dt}}+{a}_{\mathrm{0}} \Psi=\mathrm{0} \\ $$$${Is}\:{it}\:{solvable}??? \\ $$

Question Number 114721 Answers: 2 Comments: 0

....nice calculus.... prove that:: Φ=∫_(0 ) ^( 1) xln[ln(x).ln(1−x)]dx=−γ γ ::= euler mascheroni constant. ...m.n.july.1970...

$$\:\:\:\:\:\:\:\:\:\:....{nice}\:\:{calculus}.... \\ $$$$\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Phi=\int_{\mathrm{0}\:} ^{\:\mathrm{1}} {xln}\left[{ln}\left({x}\right).{ln}\left(\mathrm{1}−{x}\right)\right]{dx}=−\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\gamma\:::=\:{euler}\:\:{mascheroni}\:{constant}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Question Number 114720 Answers: 2 Comments: 0

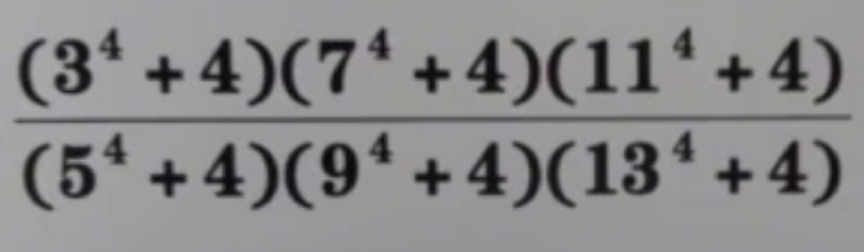
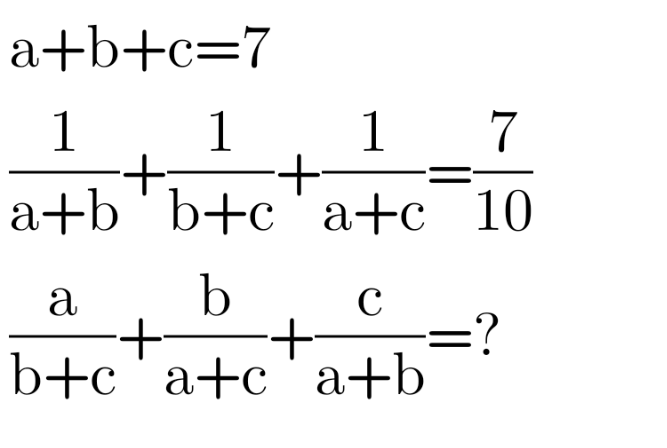
Question Number 114710 Answers: 1 Comments: 0

Question Number 114709 Answers: 1 Comments: 1

Question Number 114708 Answers: 0 Comments: 1

Question Number 114706 Answers: 1 Comments: 1

Question Number 114699 Answers: 1 Comments: 1

∫_0 ^(π/2) (dx/( (√(1+tan^4 x)))) ?

$$\:\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}}}\:? \\ $$

Question Number 114696 Answers: 1 Comments: 0

lim_(x→0) ((sinh (2x)−sin 2x)/x^5 ) =?

$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sinh}\:\left(\mathrm{2}{x}\right)−\mathrm{sin}\:\mathrm{2}{x}}{{x}^{\mathrm{5}} }\:=? \\ $$

Question Number 114689 Answers: 1 Comments: 0

∫xsin^n xdx

$$\int{xsin}^{{n}} {xdx} \\ $$

Question Number 114682 Answers: 1 Comments: 0

Question Number 114681 Answers: 3 Comments: 0

Prove that ∫_0 ^∞ (x^n /(e^x −1))dx=n!ζ(n+1)

$${Prove}\:{that}\:\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{n}} }{{e}^{{x}} −\mathrm{1}}{dx}={n}!\zeta\left({n}+\mathrm{1}\right) \\ $$

Question Number 114676 Answers: 1 Comments: 0

If a^(1/2) −a^(−(1/2)) =1, prove that a+a^(−1) =3

$$\mathrm{If}\:{a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{a}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1},\:\mathrm{prove}\:\mathrm{that}\:{a}+{a}^{−\mathrm{1}} =\mathrm{3} \\ $$

Question Number 114673 Answers: 0 Comments: 1

★ x^3 −x−(1/6)=0 ⇒ x=?

$$\:\:\:\:\bigstar\:\:\:\mathrm{x}^{\mathrm{3}} −\mathrm{x}−\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{0}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{x}=? \\ $$

Question Number 114671 Answers: 1 Comments: 0

Integrate ∫ ((x^4 +x^(−4) )/(x^6 +x^(−6) ))dx

$$ \\ $$$$\:\mathrm{Integrate}\:\:\int\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{−\mathrm{4}} }{\mathrm{x}^{\mathrm{6}} +\mathrm{x}^{−\mathrm{6}} }\mathrm{dx} \\ $$

Question Number 114668 Answers: 1 Comments: 0

((x+(√(x^2 −1)))/(x−(√(x^2 −1)))) + ((x−(√(x^2 −1)))/(x+(√(x^2 −1)))) = 98

$$\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:+\:\frac{{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\:\mathrm{98}\: \\ $$

Pg 1030 Pg 1031 Pg 1032 Pg 1033 Pg 1034 Pg 1035 Pg 1036 Pg 1037 Pg 1038 Pg 1039

Terms of Service

Contact: info@tinkutara.com