
AllQuestion and Answers: Page 1030
Question Number 117250 Answers: 1 Comments: 0
Question Number 117249 Answers: 1 Comments: 0
Question Number 117243 Answers: 1 Comments: 1

Question Number 117228 Answers: 1 Comments: 0
Question Number 117227 Answers: 0 Comments: 0
Question Number 117223 Answers: 1 Comments: 0
Question Number 117221 Answers: 3 Comments: 1
Question Number 117295 Answers: 1 Comments: 0

Question Number 117207 Answers: 0 Comments: 2
Question Number 117286 Answers: 2 Comments: 0
Question Number 117205 Answers: 0 Comments: 0
Question Number 117204 Answers: 1 Comments: 2

Question Number 117215 Answers: 0 Comments: 1
Question Number 117192 Answers: 1 Comments: 0
Question Number 117191 Answers: 0 Comments: 0
$$\int\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$
Question Number 117188 Answers: 2 Comments: 1
Question Number 117176 Answers: 4 Comments: 1
Question Number 117172 Answers: 1 Comments: 0
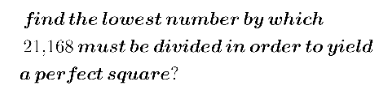
Question Number 117171 Answers: 1 Comments: 0
Question Number 117164 Answers: 2 Comments: 0
Question Number 117163 Answers: 2 Comments: 0
Question Number 117144 Answers: 1 Comments: 0
Question Number 117143 Answers: 1 Comments: 0

Question Number 117142 Answers: 0 Comments: 0

Question Number 117140 Answers: 1 Comments: 0

Question Number 117216 Answers: 1 Comments: 0
Pg 1025 Pg 1026 Pg 1027 Pg 1028 Pg 1029 Pg 1030 Pg 1031 Pg 1032 Pg 1033 Pg 1034
