Question and Answers Forum

AllQuestion and Answers: Page 1029

Question Number 116939 Answers: 2 Comments: 0

prof if the limitf(x)=L and limit f(x)=M,then L=M

$${prof}\:\:{if}\:\:{the}\:{limitf}\left({x}\right)={L}\:{and}\: \\ $$$${limit}\:{f}\left({x}\right)={M},{then}\:{L}={M} \\ $$

Question Number 116930 Answers: 2 Comments: 1

Given f(x)=5^(√x) find f ′(x) by using limit (first principal derivative)

$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{5}^{\sqrt{\mathrm{x}}} \:\mathrm{find}\:\mathrm{f}\:'\left(\mathrm{x}\right)\:\mathrm{by}\:\mathrm{using}\:\mathrm{limit} \\ $$$$\left(\mathrm{first}\:\mathrm{principal}\:\mathrm{derivative}\right) \\ $$

Question Number 116941 Answers: 0 Comments: 8

prove that 7×8=7+8=78

$${prove}\:{that}\:\mathrm{7}×\mathrm{8}=\mathrm{7}+\mathrm{8}=\mathrm{78} \\ $$

Question Number 116921 Answers: 1 Comments: 0

Question Number 116917 Answers: 1 Comments: 0

Find the greatest coefficient and greatest term in (3x − 2)^(− 7) . Sir is it: (− 1)^(− 7) .(2 − 3x)^(− 7) = − (2 − 3x)^(− 7) = − ((8008 × 2^(10) )/3^(17) )

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{and}\:\mathrm{greatest}\:\mathrm{term}\:\mathrm{in} \\ $$$$\left(\mathrm{3x}\:\:−\:\:\mathrm{2}\right)^{−\:\mathrm{7}} . \\ $$$$ \\ $$$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{it}:\:\:\:\:\:\left(−\:\mathrm{1}\right)^{−\:\mathrm{7}} .\left(\mathrm{2}\:\:−\:\:\mathrm{3x}\right)^{−\:\mathrm{7}} \:\:\:\:=\:\:\:−\:\left(\mathrm{2}\:\:−\:\:\mathrm{3x}\right)^{−\:\mathrm{7}} \\ $$$$=\:\:\:−\:\:\frac{\mathrm{8008}\:\:×\:\:\mathrm{2}^{\mathrm{10}} }{\mathrm{3}^{\mathrm{17}} } \\ $$

Question Number 116915 Answers: 2 Comments: 0

Question Number 116913 Answers: 1 Comments: 0

Question Number 116907 Answers: 2 Comments: 0

Question Number 116903 Answers: 2 Comments: 0

Question Number 116902 Answers: 0 Comments: 0

Question Number 116900 Answers: 0 Comments: 0

Question Number 116891 Answers: 2 Comments: 0

Proof that ((4(cos^4 (a)+sin^4 (a)))/(cos^4 (a)−sin^4 (a))) = (3+cos (4a))sec (2a)

$$\mathrm{Proof}\:\mathrm{that}\:\frac{\mathrm{4}\left(\mathrm{cos}\:^{\mathrm{4}} \left({a}\right)+\mathrm{sin}\:^{\mathrm{4}} \left({a}\right)\right)}{\mathrm{cos}\:^{\mathrm{4}} \left({a}\right)−\mathrm{sin}\:^{\mathrm{4}} \left({a}\right)}\:=\:\left(\mathrm{3}+\mathrm{cos}\:\left(\mathrm{4}{a}\right)\right)\mathrm{sec}\:\left(\mathrm{2}{a}\right)\: \\ $$

Question Number 116887 Answers: 2 Comments: 1

Let k=sin 1°×sin 3°×sin 5°×…×sin 89° Find log_2 k^2 .

$$\mathrm{Let}\:{k}=\mathrm{sin}\:\mathrm{1}°×\mathrm{sin}\:\mathrm{3}°×\mathrm{sin}\:\mathrm{5}°×\ldots×\mathrm{sin}\:\mathrm{89}° \\ $$$$\mathrm{Find}\:\mathrm{log}_{\mathrm{2}} {k}^{\mathrm{2}} . \\ $$

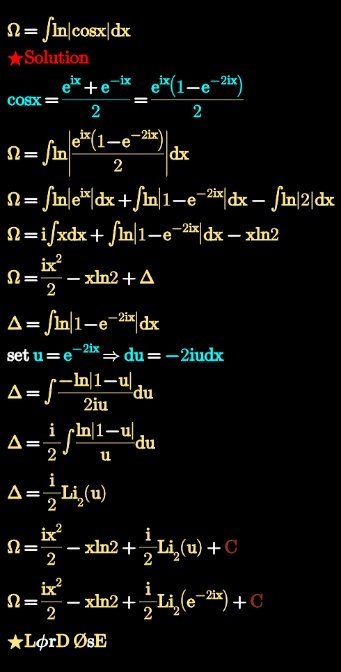
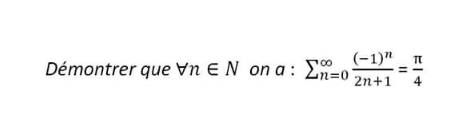
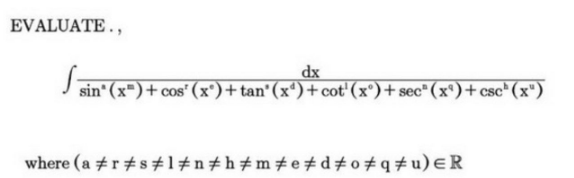
Question Number 116884 Answers: 1 Comments: 0

Question Number 116883 Answers: 1 Comments: 0

Find the number m of ways to partition 10 students into four team so that two team contains 3 students and two team contains 2 students .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{m}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{to} \\ $$$$\mathrm{partition}\:\mathrm{10}\:\mathrm{students}\:\mathrm{into}\:\mathrm{four}\:\mathrm{team} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{two}\:\mathrm{team}\:\mathrm{contains}\:\mathrm{3}\:\mathrm{students} \\ $$$$\mathrm{and}\:\mathrm{two}\:\mathrm{team}\:\mathrm{contains}\:\mathrm{2}\:\mathrm{students}\:. \\ $$

Question Number 116881 Answers: 3 Comments: 0

Find the number m of non negative integer solution of x+y+z=18

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{m}\:\mathrm{of}\:\mathrm{non}\:\mathrm{negative} \\ $$$$\mathrm{integer}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{18} \\ $$$$ \\ $$

Question Number 116859 Answers: 2 Comments: 1

lim_(x→∞) ((3x^2 )/5^x )=?

$${li}\underset{{x}\rightarrow\infty} {{m}}\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{5}^{{x}} }=? \\ $$

Question Number 116854 Answers: 4 Comments: 0

... calculus elementary algebra ... please solve :: ((6x+9))^(1/3) +((7−7x))^(1/3) +((x−8))^(1/3) =2 ...m.n.july.1970...

$$\:\:\:...\:\:\:{calculus}\:\:\:{elementary}\:\:{algebra}\:...\:\: \\ $$$$ \\ $$$$ \\ $$$$\:{please}\:{solve}\::: \\ $$$$ \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{6}{x}+\mathrm{9}}\:+\sqrt[{\mathrm{3}}]{\mathrm{7}−\mathrm{7}{x}}\:+\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:=\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$$$\: \\ $$

Question Number 116853 Answers: 0 Comments: 0

Question Number 116847 Answers: 1 Comments: 1

Question Number 116846 Answers: 0 Comments: 2

...nice calculus... prove that :: ∫_0 ^( (π/2)) (√(((2^x −1)sin^3 (x))/((2^x +1)(sin^3 (x)+cos^3 (x))))) dx<(π/8) ...m.n.1970...

$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:{prove}\:\:{that}\::: \\ $$$$ \\ $$$$\:\: \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\left(\mathrm{2}^{{x}} −\mathrm{1}\right){sin}^{\mathrm{3}} \left({x}\right)}{\left(\mathrm{2}^{{x}} +\mathrm{1}\right)\left({sin}^{\mathrm{3}} \left({x}\right)+{cos}^{\mathrm{3}} \left({x}\right)\right)}}\:\:{dx}<\frac{\pi}{\mathrm{8}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}.\mathrm{1970}... \\ $$$$ \\ $$

Question Number 116845 Answers: 1 Comments: 1

Question Number 116844 Answers: 1 Comments: 0

∫ ((8x+sin^(−1) (2x))/( (√(1−4x^2 )))) dx

$$\int\:\frac{\mathrm{8x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$

Question Number 116843 Answers: 0 Comments: 1

Question Number 116841 Answers: 0 Comments: 1

Question Number 116832 Answers: 3 Comments: 0

If 19 sin 2x = 37 cos 2x+38 sin^2 x then tan x = __

$$\mathrm{If}\:\mathrm{19}\:\mathrm{sin}\:\mathrm{2x}\:=\:\mathrm{37}\:\mathrm{cos}\:\mathrm{2x}+\mathrm{38}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{then}\:\mathrm{tan}\:\mathrm{x}\:=\:\_\_ \\ $$

Pg 1024 Pg 1025 Pg 1026 Pg 1027 Pg 1028 Pg 1029 Pg 1030 Pg 1031 Pg 1032 Pg 1033

Contact: info@tinkutara.com