Question and Answers Forum

AllQuestion and Answers: Page 1017

Question Number 118822 Answers: 2 Comments: 0

In how many ways can the letters of the word LEVITATE be arranged if the vowels must not be next to each other

$$\:\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{the}\:\mathrm{letters}\:\mathrm{of}\: \\ $$$$\:\mathrm{the}\:\mathrm{word}\:{LEVITATE}\:\mathrm{be}\:\mathrm{arranged}\:\mathrm{if} \\ $$$$\:\mathrm{the}\:\mathrm{vowels}\:\mathrm{must}\:\mathrm{not}\:\mathrm{be}\:\mathrm{next}\:\mathrm{to}\:\mathrm{each} \\ $$$$\:\mathrm{other} \\ $$

Question Number 118819 Answers: 3 Comments: 0

∫((x^4 +x^2 +1)/((x^2 +4)^2 (x^2 +1))) dx

$$\int\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:{dx}\: \\ $$

Question Number 118813 Answers: 1 Comments: 0

(d^2 y/dx^2 ) −4x (dy/dx) + y(3x^2 −2)= 0

$$\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:−\mathrm{4}{x}\:\frac{{dy}}{{dx}}\:+\:{y}\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}\right)=\:\mathrm{0}\: \\ $$

Question Number 118811 Answers: 1 Comments: 4

Question Number 118810 Answers: 3 Comments: 0

(√(2003)) + (√(2005)) < 2(√(2004)) ???

$$\sqrt{\mathrm{2003}}\:+\:\sqrt{\mathrm{2005}}\:<\:\mathrm{2}\sqrt{\mathrm{2004}}\:\:??? \\ $$

Question Number 118798 Answers: 2 Comments: 0

1)Find (dy/dx) ; if x = at^2 , y = 2at 2)

$$\left.\:\mathrm{1}\right){Find}\:\frac{{dy}}{{dx}}\:\:;\:\:\:{if}\:\:\:{x}\:=\:{at}^{\mathrm{2}} \:,\:\:{y}\:=\:\mathrm{2}{at} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\: \\ $$

Question Number 118793 Answers: 0 Comments: 0

Question Number 118791 Answers: 2 Comments: 0

Question Number 118790 Answers: 0 Comments: 0

Show by recurence that (a+b)^n =Σ_(k=0 ) ^n C_n ^k ×a^k ×b^(n−k)

$$\mathrm{Show}\:\mathrm{by}\:\mathrm{recurence}\:\mathrm{that} \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}\:} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} ×\mathrm{a}^{\mathrm{k}} ×\mathrm{b}^{\mathrm{n}−\mathrm{k}} \\ $$

Question Number 118781 Answers: 0 Comments: 6

Question Number 118780 Answers: 2 Comments: 0

z and z′ ∈ C . show that: 1. zz′^(−) =z^− ×z′^(−) 2. ((z/(z′)))^(−) =(z^− /(z′^(−) ))

$$\mathrm{z}\:\mathrm{and}\:\mathrm{z}'\:\in\:\mathbb{C}\:. \\ $$$$\mathrm{show}\:\mathrm{that}: \\ $$$$\mathrm{1}.\:\:\:\:\:\:\overline {\mathrm{zz}'}=\overset{−} {\mathrm{z}}×\overline {\mathrm{z}'} \\ $$$$\mathrm{2}.\:\:\:\:\:\:\:\overline {\left(\frac{\mathrm{z}}{\mathrm{z}'}\right)}=\frac{\overset{−} {\mathrm{z}}}{\overline {\mathrm{z}'}} \\ $$$$ \\ $$

Question Number 118777 Answers: 1 Comments: 0

lim_(n→∞) (((n!)/n^n ))^(1/n) =lim_(n→∞) ((((√(2nπ)) n^n )/(n^n ×e^n )))^(1/n) ⇒lim_(n→∞) (1/e)((√(2nπ)))^(1/n) =(1/e)

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}!}{{n}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{2}{n}\pi}\:{n}^{{n}} }{{n}^{{n}} ×{e}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{e}}\left(\sqrt{\mathrm{2}{n}\pi}\right)^{\frac{\mathrm{1}}{{n}}} =\frac{\mathrm{1}}{{e}} \\ $$

Question Number 207634 Answers: 1 Comments: 0

calculer lim n→+oo f_n (x) f_n (x)=∫_0^ ^(+oo) ((ne^(−x) )/(1+nx))dx /x∈[0+oo[

$${calculer}\:{lim}\:\:{n}\rightarrow+{oo}\:{f}_{{n}} \left({x}\right) \\ $$$${f}_{{n}} \left({x}\right)=\int_{\mathrm{0}^{} } ^{+{oo}} \frac{{ne}^{−{x}} }{\mathrm{1}+{nx}}{dx}\:\:\:/{x}\in\left[\mathrm{0}+{oo}\left[\right.\right. \\ $$

Question Number 118768 Answers: 1 Comments: 0

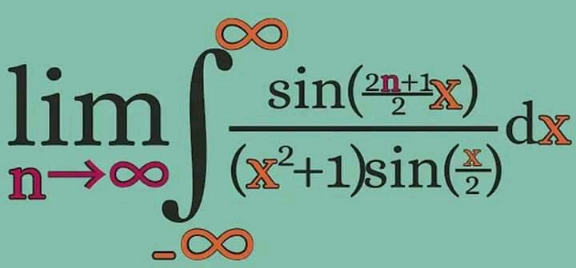
Question Number 118759 Answers: 0 Comments: 4

The first three terms in the binomial expansion (p−q)^m , in ascending order of q, are denoted by a,b and c respectively. Show that (b^2 /(ac))=((2m)/(m−1))

$$\mathrm{The}\:\mathrm{first}\:\mathrm{three}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{binomial}\:\mathrm{expansion} \\ $$$$\left({p}−{q}\right)^{{m}} \:,\:\mathrm{in}\:\mathrm{ascending}\:\mathrm{order}\:\mathrm{of}\:{q},\:\mathrm{are}\:\mathrm{denoted} \\ $$$$\mathrm{by}\:{a},{b}\:\mathrm{and}\:{c}\:\mathrm{respectively}. \\ $$$$\mathrm{Show}\:\mathrm{that}\:\frac{{b}^{\mathrm{2}} }{{ac}}=\frac{\mathrm{2}{m}}{{m}−\mathrm{1}} \\ $$

Question Number 118757 Answers: 2 Comments: 1

Question Number 118753 Answers: 3 Comments: 1

∫_2 ^4 x^3 e^x dx

$$\int_{\mathrm{2}} ^{\mathrm{4}} {x}^{\mathrm{3}} {e}^{{x}} {dx} \\ $$

Question Number 118752 Answers: 0 Comments: 0

∫ ((2 dx)/(x^2 (((3+x^4 )^5 ))^(1/(4 )) )) dx

$$\:\:\int\:\frac{\mathrm{2}\:{dx}}{{x}^{\mathrm{2}} \:\sqrt[{\mathrm{4}\:}]{\left(\mathrm{3}+{x}^{\mathrm{4}} \right)^{\mathrm{5}} }}\:{dx}\: \\ $$

Question Number 118747 Answers: 4 Comments: 0

find the distance of point (2,1,−2) to plane passing through points (−1,2,−3); (0,−4,−2) and (1,3,4).

$${find}\:{the}\:{distance}\:{of}\:{point}\:\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right)\:{to}\:{plane} \\ $$$${passing}\:{through}\:{points}\:\left(−\mathrm{1},\mathrm{2},−\mathrm{3}\right); \\ $$$$\left(\mathrm{0},−\mathrm{4},−\mathrm{2}\right)\:{and}\:\left(\mathrm{1},\mathrm{3},\mathrm{4}\right). \\ $$

Question Number 118740 Answers: 1 Comments: 1

f(x+2)+f(x−1)=2x^2 +14 f(x)=?

$${f}\left({x}+\mathrm{2}\right)+{f}\left({x}−\mathrm{1}\right)=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14} \\ $$$${f}\left({x}\right)=? \\ $$

Question Number 118733 Answers: 4 Comments: 1

Question Number 118727 Answers: 0 Comments: 0

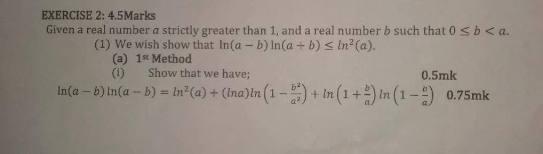
Question Number 118712 Answers: 4 Comments: 0

Prove the following inequalities: 1)(((n+1)/2))^n >n! for ∀n∈N^∗ ,n>1 2)∣sinnx∣≤n∣sinx∣ for ∀n∈N^∗

$$\mathrm{Prove}\:\mathrm{the}\:\mathrm{following}\:\mathrm{inequalities}: \\ $$$$\left.\mathrm{1}\right)\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} >\mathrm{n}!\:\mathrm{for}\:\forall\mathrm{n}\in\mathrm{N}^{\ast} ,\mathrm{n}>\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\mid\mathrm{sinnx}\mid\leqslant\mathrm{n}\mid\mathrm{sinx}\mid\:\mathrm{for}\:\forall\mathrm{n}\in\mathrm{N}^{\ast} \\ $$

Question Number 118711 Answers: 0 Comments: 1

Ripasso di matematica per la verifica L′addizione non gode della proprieta^ invariantiva 7+11=(7−3)+(11−3) FALSO Proprieta^ distributiva della moltiplicazione rispetto alla sottrazione 5•(6−4)=30−20 Risolvere la seguente espressione [(2+1)^4 •2^7 •3^3 ]:(6^(10) :6^8 )^3 −6=[3^4 •2^7 •3^3 ]:(6^2 )^3 −6=[3^7 •2^7 ]:6^6 −6= =6^7 :6^6 −6 Es. 184 pag.31 {[2+2•(5+4)•(8−5)]:(4•7)}^5 ={[2+2•9•3]:28}^5 ={[2+54]:28}^5 ={56:28}^5 = {2}^5 =2^5 =32

$$\mathrm{Ripasso}\:\mathrm{di}\:\mathrm{matematica}\:\mathrm{per}\:\mathrm{la}\:\mathrm{verifica} \\ $$$$\mathrm{L}'\mathrm{addizione}\:\mathrm{non}\:\mathrm{gode}\:\mathrm{della}\:\mathrm{propriet}\acute {\mathrm{a}}\:\mathrm{invariantiva} \\ $$$$\mathrm{7}+\mathrm{11}=\left(\mathrm{7}−\mathrm{3}\right)+\left(\mathrm{11}−\mathrm{3}\right)\:\:\:\:\mathrm{FALSO} \\ $$$$\mathrm{Propriet}\acute {\mathrm{a}}\:\mathrm{distributiva}\:\mathrm{della}\:\mathrm{moltiplicazione}\:\mathrm{rispetto}\:\mathrm{alla}\:\mathrm{sottrazione} \\ $$$$\mathrm{5}\bullet\left(\mathrm{6}−\mathrm{4}\right)=\mathrm{30}−\mathrm{20} \\ $$$$\mathrm{Risolvere}\:\mathrm{la}\:\mathrm{seguente}\:\mathrm{espressione} \\ $$$$\left[\left(\mathrm{2}+\mathrm{1}\right)^{\mathrm{4}} \bullet\mathrm{2}^{\mathrm{7}} \bullet\mathrm{3}^{\mathrm{3}} \right]:\left(\mathrm{6}^{\mathrm{10}} :\mathrm{6}^{\mathrm{8}} \right)^{\mathrm{3}} −\mathrm{6}=\left[\mathrm{3}^{\mathrm{4}} \bullet\mathrm{2}^{\mathrm{7}} \bullet\mathrm{3}^{\mathrm{3}} \right]:\left(\mathrm{6}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{6}=\left[\mathrm{3}^{\mathrm{7}} \bullet\mathrm{2}^{\mathrm{7}} \right]:\mathrm{6}^{\mathrm{6}} −\mathrm{6}= \\ $$$$=\mathrm{6}^{\mathrm{7}} :\mathrm{6}^{\mathrm{6}} −\mathrm{6} \\ $$$$\mathrm{Es}.\:\mathrm{184}\:\mathrm{pag}.\mathrm{31} \\ $$$$\left\{\left[\mathrm{2}+\mathrm{2}\bullet\left(\mathrm{5}+\mathrm{4}\right)\bullet\left(\mathrm{8}−\mathrm{5}\right)\right]:\left(\mathrm{4}\bullet\mathrm{7}\right)\right\}^{\mathrm{5}} =\left\{\left[\mathrm{2}+\mathrm{2}\bullet\mathrm{9}\bullet\mathrm{3}\right]:\mathrm{28}\right\}^{\mathrm{5}} =\left\{\left[\mathrm{2}+\mathrm{54}\right]:\mathrm{28}\right\}^{\mathrm{5}} =\left\{\mathrm{56}:\mathrm{28}\right\}^{\mathrm{5}} = \\ $$$$\left\{\mathrm{2}\right\}^{\mathrm{5}} =\mathrm{2}^{\mathrm{5}} =\mathrm{32} \\ $$

Question Number 118710 Answers: 2 Comments: 0

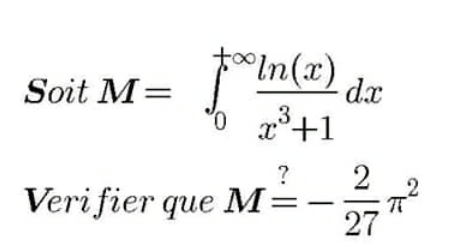
Question Number 118705 Answers: 2 Comments: 0

... ⧫Advanced Calculus⧫... Evaluate:: Ω = ∫_0 ^( 1 ) ((sin^(−1) (x))/(1+x^2 ))dx ...♠L𝛗rD ∅sE♠... ...♣GooD LucK♣

$$ \\ $$$$ \\ $$$$...\:\blacklozenge\mathrm{Advanced}\:\mathrm{Calculus}\blacklozenge... \\ $$$$ \\ $$$$\mathrm{Evaluate}:: \\ $$$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{1}\:} \frac{\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$ \\ $$$$...\spadesuit\boldsymbol{\mathrm{L}\phi\mathrm{rD}}\:\boldsymbol{\varnothing\mathrm{sE}}\spadesuit... \\ $$$$ \\ $$$$...\clubsuit\boldsymbol{\mathrm{GooD}}\:\boldsymbol{\mathrm{LucK}}\clubsuit \\ $$

Pg 1012 Pg 1013 Pg 1014 Pg 1015 Pg 1016 Pg 1017 Pg 1018 Pg 1019 Pg 1020 Pg 1021

Contact: [email protected]