
AllQuestion and Answers: Page 1013
Question Number 119257 Answers: 0 Comments: 0
Question Number 119256 Answers: 0 Comments: 0
Question Number 119253 Answers: 2 Comments: 0
Question Number 119250 Answers: 1 Comments: 5

Question Number 119246 Answers: 2 Comments: 0
Question Number 119241 Answers: 1 Comments: 0
Question Number 119240 Answers: 2 Comments: 0
Question Number 119235 Answers: 1 Comments: 0
Question Number 119233 Answers: 3 Comments: 0
$$\:\left({D}^{\mathrm{2}} −\mathrm{5}{D}+\mathrm{6}\right){y}\:=\:{e}^{\mathrm{3}{x}} \\ $$
Question Number 119229 Answers: 3 Comments: 0
Question Number 119220 Answers: 2 Comments: 0
Question Number 119216 Answers: 4 Comments: 4
Question Number 119214 Answers: 1 Comments: 0
Question Number 119212 Answers: 1 Comments: 0

Question Number 119204 Answers: 0 Comments: 0
Question Number 119193 Answers: 3 Comments: 3
Question Number 119192 Answers: 1 Comments: 0

Question Number 119187 Answers: 0 Comments: 3

Question Number 119184 Answers: 0 Comments: 0
Question Number 119173 Answers: 3 Comments: 0
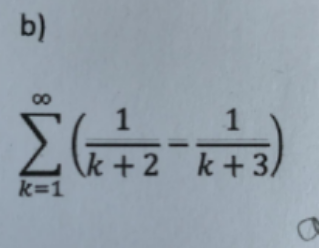
Question Number 119164 Answers: 0 Comments: 0

Question Number 119160 Answers: 0 Comments: 5

Question Number 119159 Answers: 2 Comments: 0
Question Number 119158 Answers: 1 Comments: 0
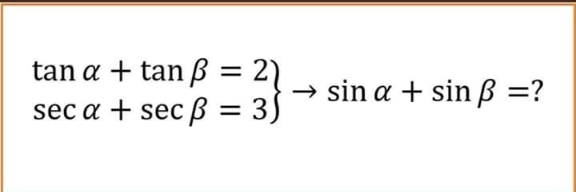
Question Number 119157 Answers: 2 Comments: 0

Question Number 119155 Answers: 1 Comments: 5

Pg 1008 Pg 1009 Pg 1010 Pg 1011 Pg 1012 Pg 1013 Pg 1014 Pg 1015 Pg 1016 Pg 1017
